Calendar Logic

"What is false one day may become true the next day." –Yours Truly

Consider this statement:

"Today is a Saturday."

The statement in quotation marks is only true on Saturdays, but false every other day of the week. The negation of the statement is true every day of the week except Saturday. Therefore, the laws of logic say that a falsity can become a truth! (Vice versa is also possible!)

But there are many more date-related examples to try! Here's another statement:

"Today is Monday, Tuesday, Wednesday, Thursday, or Friday."

This statement is false during the weekends. (Saturdays & Sundays) Its negation is true during the weekends.

Here’s yet another statement; this time, let’s change the word Today to Tomorrow:

"Tomorrow is Wednesday or Friday."

This statement is true on Tuesdays & Thursdays, but false every other day of the week. This is because of the order of the weekdays; Wednesday is the next day of week after Tuesday, & Friday is the next day of week after Thursday. Its negation is true on Sundays, Mondays, Wednesdays, Fridays, & Saturdays.

Now for the next statement let’s change the word Tomorrow to Yesterday:

"Yesterday was a Sunday."

This statement is only true on Mondays; its negation is true on any day that is not a Monday. Isn’t this calendar logic simple? However, we can think bigger! Let’s bring in months, day numbers, & holidays into the mix!

The following truth calendars tell when the following statements are true or false.

P.S.: All the statements are in the image files for convenience.

Here are the yearly truth calendars:

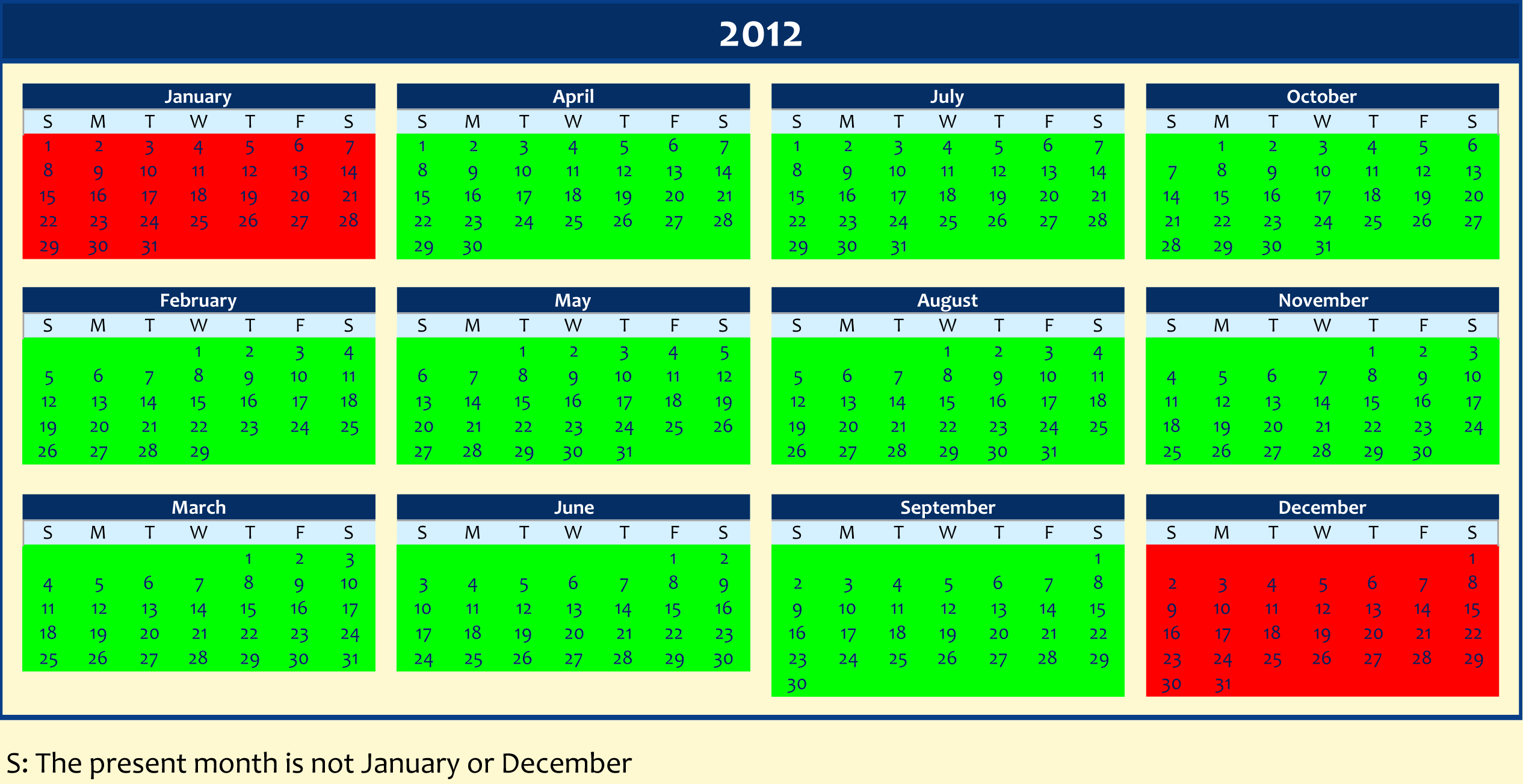
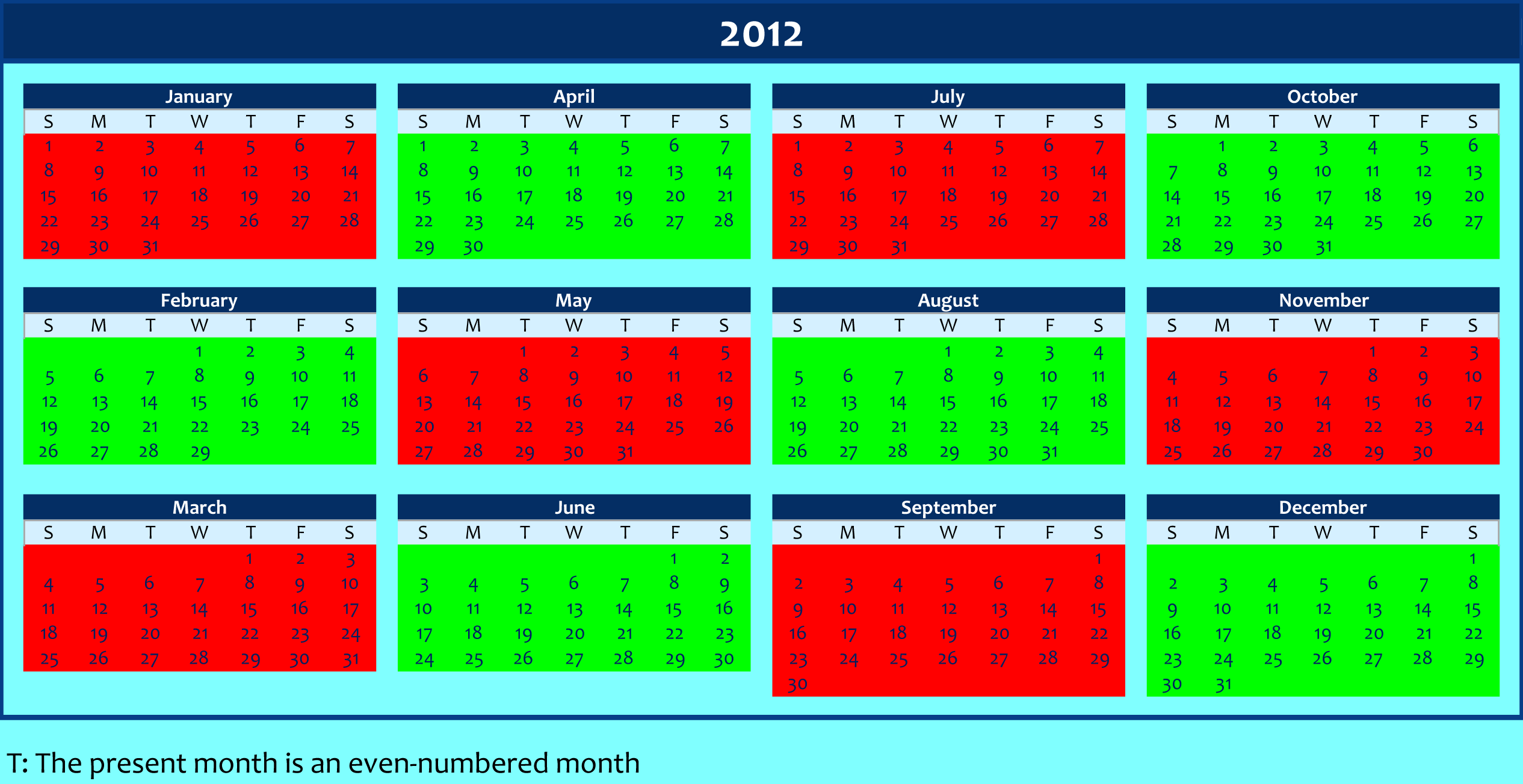
Green = True; Red = False

There are even date-related statements that are always true (Never false), like this one!

"Tomorrow is Saturday or not Saturday."

Statements like these are called tautologies. A tautology can't be used to tell a lie because it is always true, no matter what the case is.

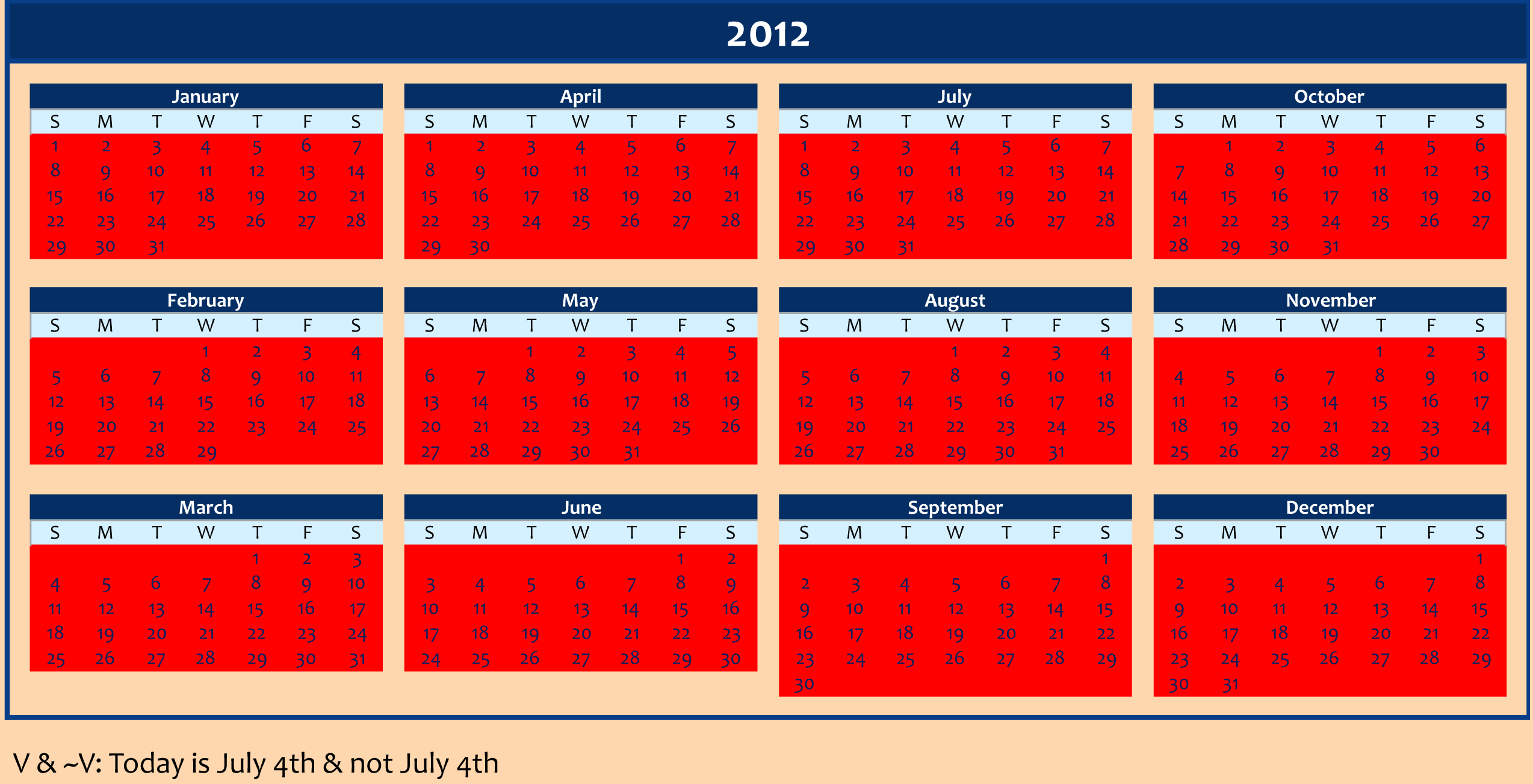
Also, there are date-related statements that are never true! (Always false) Here's an example:

"Today is July 4th & not July 4th."

Green = True; Red = False, but none of the dates or months are painted green! They're all red!

Doesn't make sense, does it? This silly statement contradicts itself! A contradiction is always false; contradiction & tautology are opposite terms by the way. If a statement is sometimes true or sometimes false, it's called a contingency.

Can you think of any more date-related statements to try? You can create truth calendars, like what you just seen on this Web page, & use simple logic to determine when the statements are true or false. Have fun!

(Brain's implication is equal to "Today is not Friday," or you can also say: "Either tomorrow is not Saturday or today is Thursday.")

Back to Index Page Back to Math Trick Menu