
Not only will you find tricks in this section, but also some tips to help you with math, & various information about numbers, logic, & geometry. Look out for my characters here, too; they'll make this section more entertaining & educating!
Here's a bonus cartoon for visiting this section:

If you can multiply big numbers with several digits quickly, then you're a super-genius! By the way, the correct answer to the math problem in the cartoon above is 5,332,114.
Here's a math tip to remember from Miss IBM:

(If the Roman numerals don't appear neatly in your Web browser, then here's the total number of math tricks: 122)
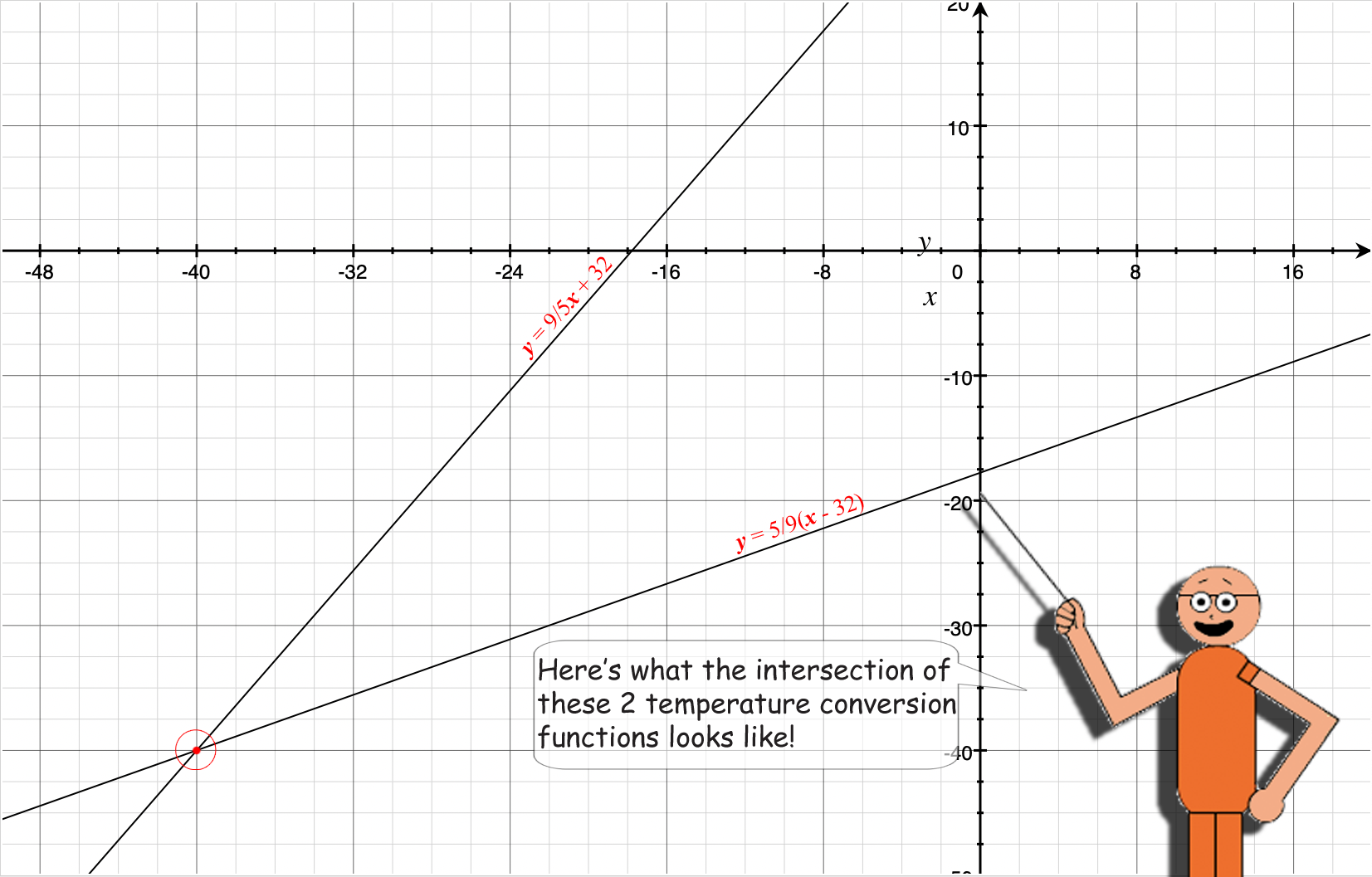
Here's a bonus fact: -40 degrees Farenheit is equal to -40 degrees Celsius!
Proof: The 2 conversion functions intersect at x = -40, y = -40
F = 9/5 × C + 32
C = 5/9(F - 32)
Another bonus fact! This is an interesting fact about the number 2, but you probably already knew it!

Another bonus fact!
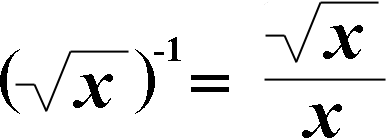
The reciprocal of a number's square root is equal to the square root divided by the original number! (x is not equal to zero!)
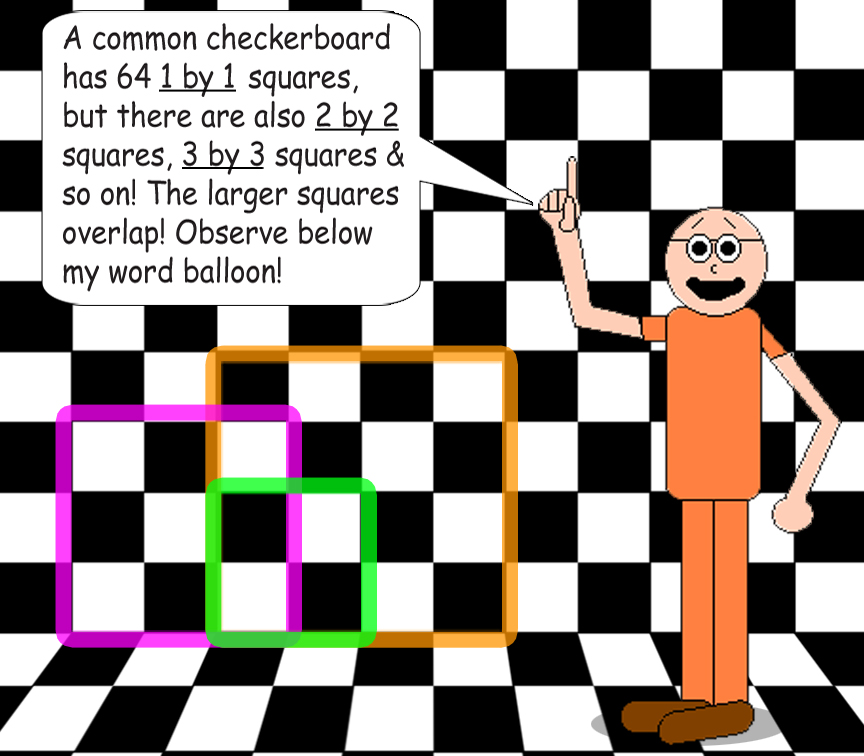
Here's a fact about checkerboards! (Or you can also call them chessboards) You can calculate how many squares a checkerboard has with the 3 formulas below:
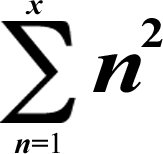
(x is also equal to the number of rows & columns!)
The 1st formula is in geometric series form, the 2nd one is in summation form and the 3rd is in cubic function form.
Here's a bonus fact about permutations & combinations:
If you pick 2 objects at a time from any set that has at least 2 objects, the permutation-to-combination ratio is always equal to 2. In other words, there will be half as many combinations as permutations.
Here's a bonus fact about the suffix -illion:
What does the suffix mean? Well, here's the -illion function!
Y = 10^(3X + 3)
X = the prefix's number, Y = the actual number
For example, 1 sexagintillion is a 1 followed by 183 zeroes! The prefix sexaginti- means "60"; 3 × 60 + 3 = 183.
Note: The number you pick for the variable x must be a counting number.
Here's the inverse of the -illion function!
X = (log(Y) - 3)/3
Click here to see the functions in Mathprint!
P.S.: About dividing by 3 in the inverse of the -illion function:
If the remainder in the quotient is 1, then Y = ten "X"-illion.
If the remainder in the quotient is 2, then Y = hundred "X"-illion.
If there's no remainder in the quotient, then Y = "X"-illion.
For example, the googol is a 1 followed by 100 zeroes, so according to the inverse of the -illion function, it's also 10 duotrigintillion since the prefix duotriginti- means "32" & (log 10100 - 3)/3 = (100 - 3)/3 = 97 ÷ 3 = 32 + 1/3; the remainder is 1 in this case.
Here's a bonus fact about imaginary/complex numbers:
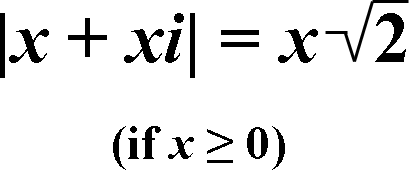
P.S.: If x is a negative number, then it's -x times the square root of 2.
Here's a bonus fact about triangles:
sin(A + B) = sin(C)
sin(B + C) = sin(A)
sin(C + A) = sin(B)
In other words, the sine of the sum of 2 angles in a triangle will always be equal to the sine of the 3rd remaining angle!
Here's a bonus fact about birth years & age, measured in full years of course:
Another bonus fact!
| If Pac-Man eats 1 ghost: | If Pac-Man eats 2 ghosts: | If Pac-Man eats 3 ghosts: | If Pac-Man eats all 4 ghosts: | |
| 1st Ghost | 200 | 200 | 200 | 200 |
| 2nd Ghost | 400 | 400 | 400 | |
| 3rd Ghost | 800 | 800 | ||
| 4th Ghost | 1600 | |||
| Sums: | 200 | 600 | 1400 | 3000 |
(This is referring to the original version of the video game)
The number of points earned for each ghost refers to this summation formula:
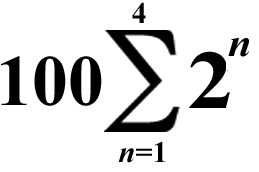
See? Even video games have math in them!
Here's a bonus fact about the Law of the Cosines:

If Angle C = 90°, then the formula simplifies to the original Pythagorean theorem (since the cosine of a right angle is zero); but if Angle C = 180°, then the formula simplifies to:
c = a + b
...Because cos(180°) = -1. (That's right! Side c simply becomes the sum of Sides a & b! However, the figure would be a straight line instead of a triangle!)
Here's a bonus fact that I call my Prime Number Test:
Example:
√(101) = 10.04987562112089...
7 is the last prime number we can pick since the next one, which is 11, is greater than the square root of 101. Therefore, 101 is a prime number!
Here's a bonus fact about fractions:

According to this cartoon, if the absolute value of the difference between the numerator & denominator is 1, then the fraction is already in its simplest terms! By the way, these 2 functions never intersect! Also, they're both discontinuous functions because of division by zero!
Here's a bonus fact about logarithms:
logxY ÷ logxZ = logzY; none of the 3 variables are equal to zero! Neither X nor Z equals 1.
Here's a bonus fact about trigonometry:
tan X = (sin X)/(cos X) = (sec X)/(csc X) = 1/(cot X)
cot X = (cos X)/(sin X) = (csc X)/(sec X) = 1/(tan X)
That's right! These are the classic Tangent & Cotangent Formulae! They both work with secants & cosecants, too! For more details, see the math tricks about trigonometry.
Here's another bonus fact about imaginary/complex numbers:
(If neither a nor b are negative, considering a + bi)
(1 + i)2 = 2i; arg(1 + i) = 45°, so arg(2i) = 90° and 45 × 2 = 90
Here's another bonus fact about logarithms:
(logxY)-1 = logYX; neither X nor Y equals 1 or 0.
Yet another bonus fact about logarithms:
log10^X(10Y) = Y/X; X ≠ 0
Note: You can substitute 10 with another number & get the same fraction! (But don't pick 0 or 1)
Here's another bonus fact:
(3i)2 ≠ 3i2; (3i)2 = -9 & 3i2 = -3
Here's a bonus fact about right isosceles triangles:
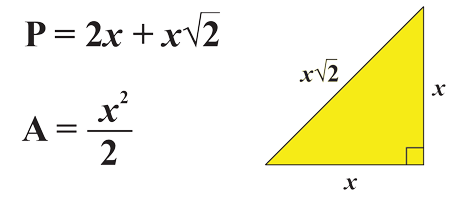
P stands for the perimeter, A stands for the area & x = the length of 1 of the 2 equal sides(also called legs).
Note: The perimeter-to-area ratio will be 1:1 if x = 4 + 2 square roots of 2; the perimeter will be 12 + 8 square roots of 2 units & the area will be 12 + 8 square roots of 2 units2!
Here's a bonus fact about the function y = x2:
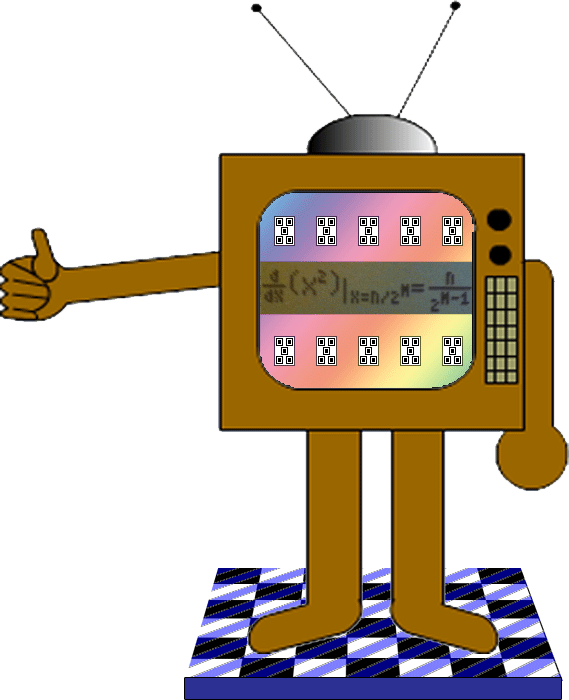
What those math symbols in T.V. Man's screen are saying is that for the function y = x2, if x is equal to a fraction that has a power of 2 as the denominator, then the numeric derivative is always equal to n/(2m-1)!
n = the numerator of your choice, m = the power of 2 of your choice, x = n/2m
Here's a bonus fact about integrals:
If B > A, then
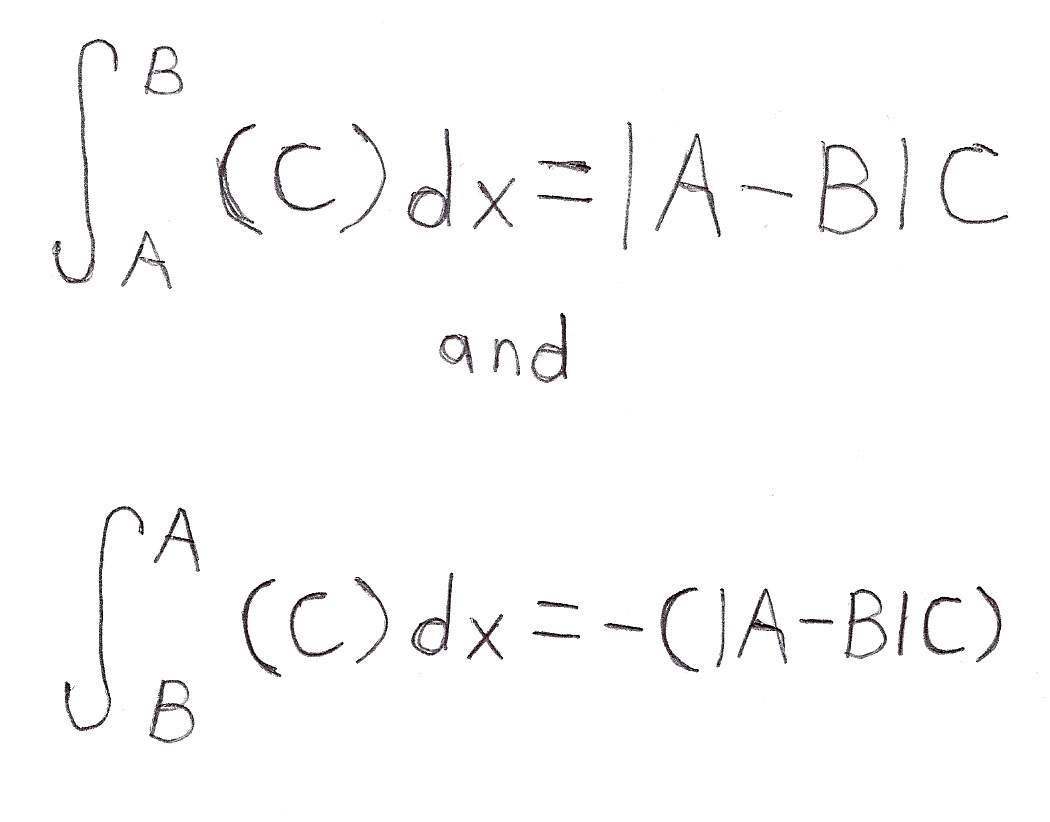
The variable C is equal to any real number you want it to be!
Here's a bonus fact about dividing fractions:
A/B ÷ C/D = (C/D ÷ A/B)-1; none of the variables are equal to zero(0)
5/3 ÷ 6/7 = 35/18 and 6/7 ÷ 5/3 = 18/35
Notice how the quotients of the division problems are reciprocals of each other! Also, by the way...
5/3 = 1 + 2/3 and 35/18 = 1 + 17/18
(The numerator isn't always less than the denominator!)
You know that raising a number to the power of -1 gives you the reciprocal, don't you? Whenever negative numbers are exponents, numerators become denominators & vice versa!
By the way, fractions can be printed horizontally or vertically. The numerator is the number on top/to the left of the vinculum & the denominator is the number on the bottom/to the right of the vinculum.
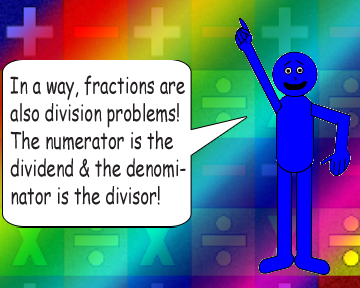
In other words, remember:
X ÷ Y = X/Y
Another thing to remember about division:
Here's another bonus fact about imaginary/complex numbers:
|1 + i| = √(2); arg(1 + i) = 45°
|2 + i| = √(5); arg(2 + i) ≈ 26.565°
(1 + i)(2 + i) = 1 + 3i; arg(1 + 3i) ≈ 71.565°; |1 + 3i| = √(10)
45° + 26.565° = 71.565° and √(2) • √(5) = √(10)
(1 + i) ÷ (2 + i) = 3/5 + 1/5i; arg(3/5 + 1/5i) ≈ 18.435°; |3/5 + 1/5i| = √(2/5)
45° - 26.565° = 18.435° and √(2) ÷ √(5) = √(2/5)
Here's another bonus fact about division & the powers of denominators of fractions:
Note: Watch the parentheses carefully!
(n/(dx+1)) ÷ (n/(dx)) = 1/d; neither d nor n are equal to zero(0)!
Here's a bonus fact about exponentiation with unit fractions:
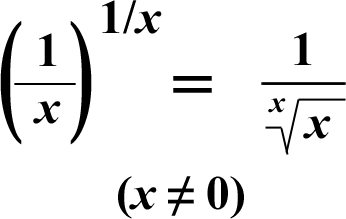
Here's a bonus fact about multplying reciprocals:
A-1B = (AB-1)-1 & AB-1 = (A-1B)-1; neither A nor B are equal to zero(0)!
Here's a bonus fact about mixed numbers:
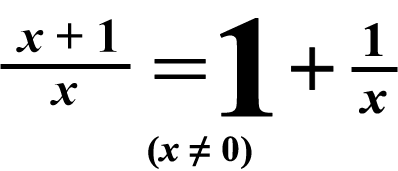
Note: Even if the variable x is not an integer, the 2 functions coincide!
If x = φ or -φ + 1, then so is y!
Here's a bonus fact to remember about negative numbers vs. positive numbers:
If X > Y, then -X < -Y
Here's a pair of bonus facts about trigonometry:
Here's a fact about the formula for the area of a circle:
D • (πR)/2 = (πD2)/4 = πR2
You can multiply the diameter by a quarter of the circumference to get the area! Also, Pi(π) times the diameter squared, divided by 4 equals Pi(π) times the radius squared!
Here's another fact about the formula for the area of a circle:
You can differentiate it to the formula for the circumference!
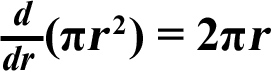
Here's a fact about the formula for the volume of a sphere:
You can differentiate it to the formula for the surface area!
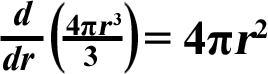
(This is like the 3-dimensional version of the fact just above this one!)
Here's a fact about linear functions:
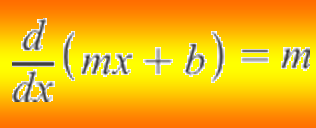
Here's a bonus fact about 2 specific functions: x2 & √(x):
x2 < x & √(x) when 1 > x > 0
Another bonus fact about logarithms:
logx((xw)y) = wy; x is equal to neither 0 nor 1 & must be positive
Here's a fact about prime numbers in fractions:
Here's a fact about differentiation:
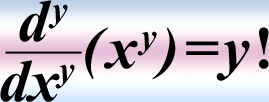
And yes, the exclamation point is representing the factorial function!
Here's a fact about function inverses:
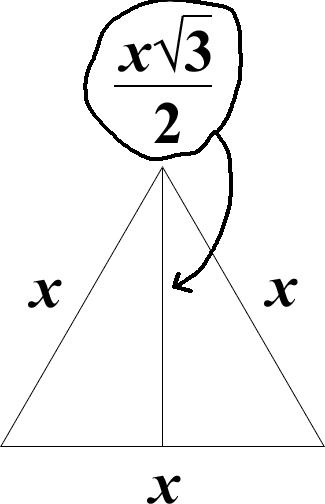
Here's a fact about equilateral triangles:
The height of an equilateral triangle is equal to half of the square root of 3 times the length of 1 of the 3 equal sides!
Here's a fact about the square roots of pure imaginary numbers:
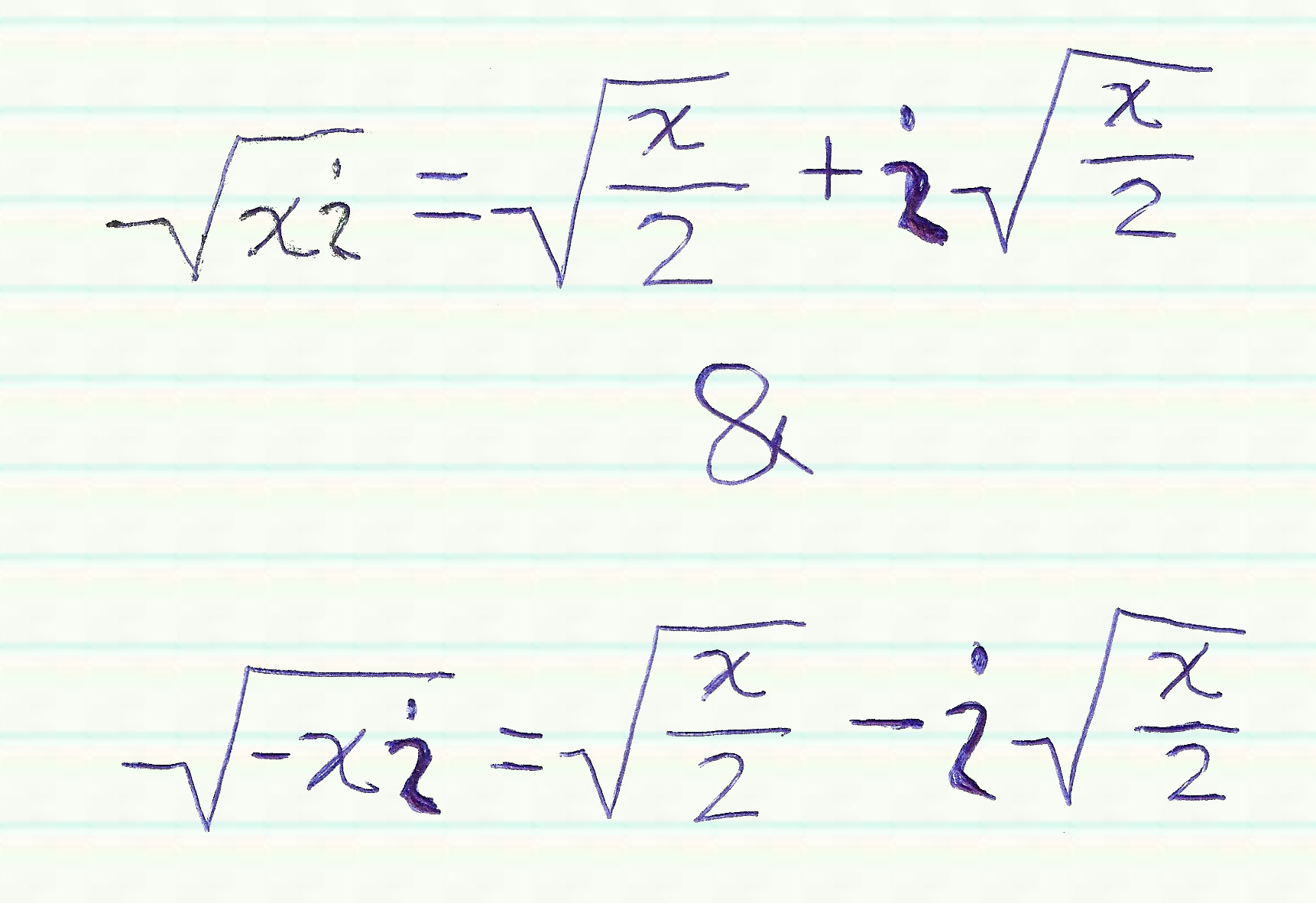
Here's another bonus fact about the Law of the Cosines:

(I know that I'm using this image twice on the same Web page, but it's about the exact same formula!)
If Angle C = 360° then the formula simplifies to:
c = b - a or -a + b
...Because cos(360°) = 1. (However, triangles never have angles that large in Euclidean geometry!)
Note: This math fact refers to Math Trick #81: Cunning Cosine!
Here's a bonus mini-comic strip about when division by zero happens in functions! (Starring Dr. John Von Foolish & Miss Zero Digit)

Here's a bonus fact about the magnitude(absolute value) of complex numbers:
|√(a) + i√(b)| = √(a + b)
Here's a bonus fact about adding 1 to the square root of 2 or subtracting 1 from the square root of 2:
(√(2) - 1)-1 = √(2) + 1 and (√(2) + 1)-1 = √(2) - 1
Notice how the reciprocals have opposite signs! The plus & minus swap places!
Here's a bonus fact about calculating any radical roots of the imaginary unit i:
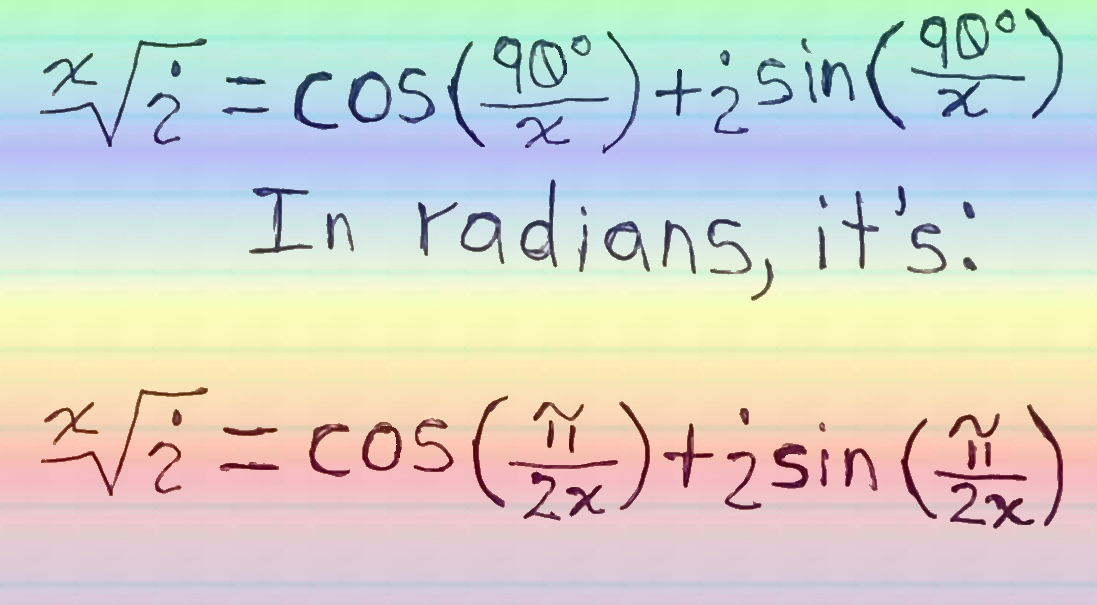
Here's a bonus fact about complex numbers in Polar form:
If the sine & cosine switch places in the Polar Form Formula, then...
R(sin(θ) + icos(θ)) = R(cos(90° - θ) + isin(90° - θ))
Here's a bonus fact about -1 & its square root i:
2x√(-1) = x√(i); x ≠ 0
(In other words, the x-th root of i is equal to the 2x-th root of -1!)
Here's a bonus fact about the arguments of complex numbers:
If a > 0 & b > 0, then arg(a + bi) + arg(b + ai) = 90°
(When both a & b are positive, the complex number is in Quadrant I!)
Here's a bonus fact about the formula for the volume of a cone:
If h = r, then the formula simplifies to: V = (πr3)/3
In other words, if the height of the cone is equal to the radius of the circular base, then you can simply cube the radius in the formula!

Here's a very interesting fact:
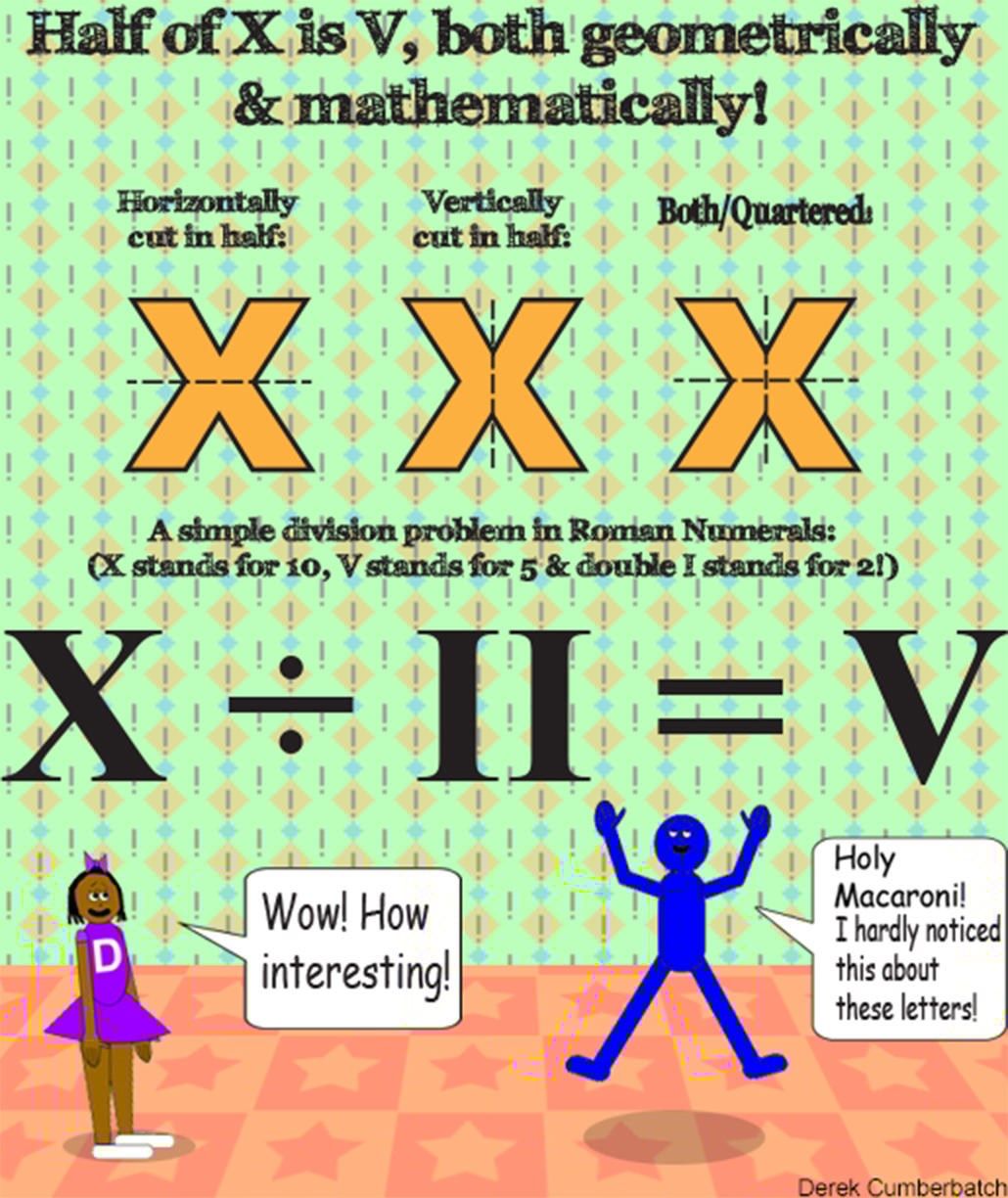
Note: V is also half of W but geometrically & if cut vertically.
Speaking of numbers, here are some Web pages with interesting facts about specific numbers:
© Derek Cumberbatch