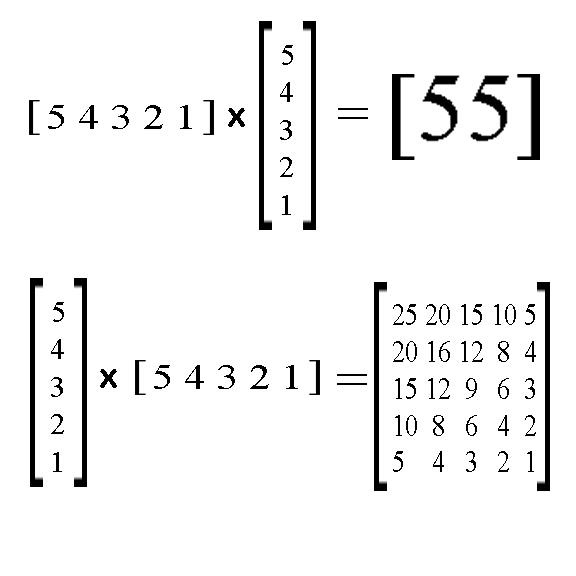Mega Matrix Multiplication

If you multiply a single row matrix by a single column matrix (or vice versa) with consecutive integers, then something quite interesting happens!

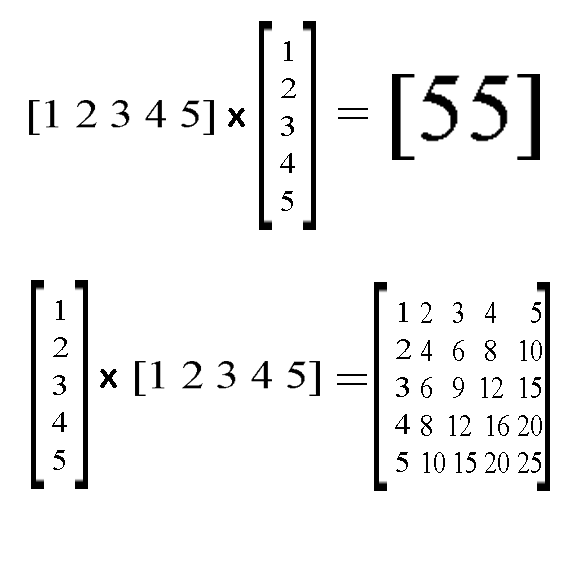
Let's call the single row matrix Matrix A & the single column matrix Matrix B. If you multiply Matrix A by Matrix B, then you get a single cell matrix with the sum of the consecutive integers' squares!

1² + 2² + 3² + ... + n² = n³/3 + n²/2 + n/6

n = the greatest integer

Note: You can also see this function on the Math Trick Menu. I call it the Checkerboard Square Total Formula! See why when you return to the Math Trick Menu!

If you multiply Matrix B by Matrix A, then you get a square matrix that is similar to a multiplication table!

There are special rules to multiplying matrices. Here are 2 examples:

The number of columns in the 1st matrix must match the number of rows in the 2nd matrix.
The matrix in the product will have the same number of rows as the 1st matrix & the same number of columns as the 2nd matrix.

Multiplication is commutative with ordinary numbers, but not with matrices because of the way they have to be multiplied...(Do you know how to multiply them? Because of how tricky it is, you'll want to use a calculator!)

If you reverse the order of the integers, you get the exact same thing if you multiply Matrix A by Matrix B. However, if you multiply Matrix B by Matrix A, then the numbers switch places in the product matrix! Observe below:

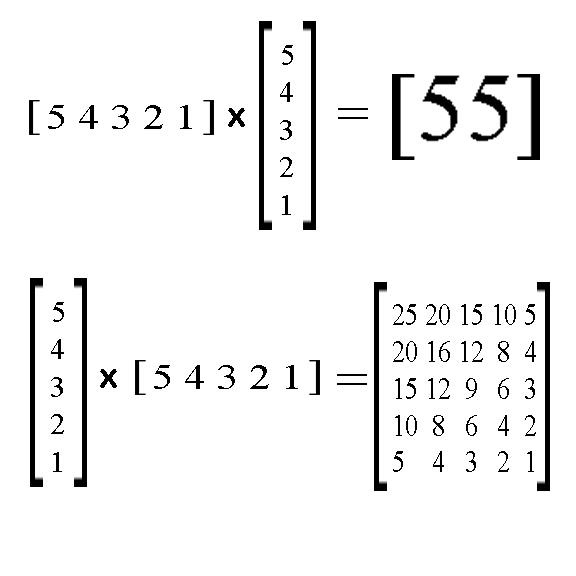
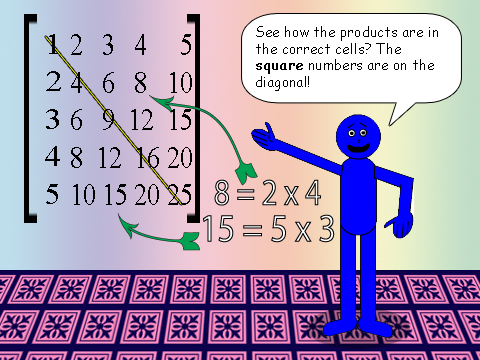
And the square numbers are still on the diagonal!

Another thing: The determinant of the "multiplication table" matrix will always be zero(0), no matter how many rows or columns it has!

Back to Index Page Back to Math Trick Menu