Types of Numbers

There are many different types of numbers, but what makes those numbers a certain type? This Web page will show you some answers to that question! It'll cover composite numbers & prime numbers, even numbers & odd numbers, rational numbers & irrational numbers, triangular numbers, & square/cube numbers.

First, Composite vs. Prime

With composite numbers, it's possible to evenly arrange objects in columns & rows of equal size. (The objects need to be equal in size, too!) For example, 24 balls can be arranged in 6 rows with 4 in each one, or 3 rows with 8 in each one, or 2 columns with 12 in each one, therefore 24 is a composite number. (The image on the left shows 6 balls per row with 24 balls; you can swap numbers with columns & rows!) However, this is impossible to do with prime numbers! A prime number of objects can only be arranged evenly in a line. For example, 13 is a prime number because if you try to arrange 13 balls with 6 in each row or column, then you get 1 oddball row or column with a remaining ball left over! It has something to do with factors; a composite number can have many factors, while prime numbers only have 2 factors: 1 & themselves. For some reason, 0 & 1 count as neither prime nor composite numbers. Non-integers aren't prime or composite either! Any prime number that is greater than 5 has either a 1, 3, 7, or 9 in the ones' column.

Even vs. Odd

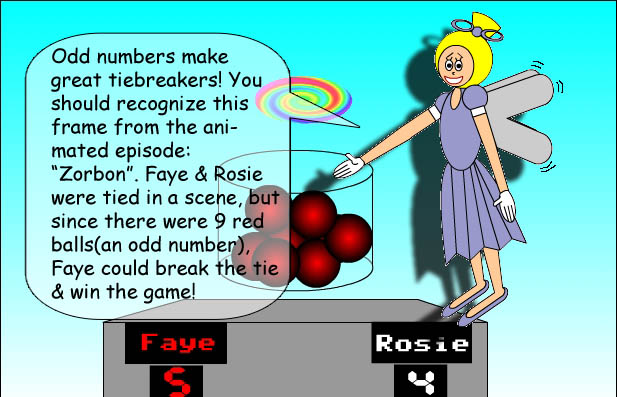As you most likely already learned, all even numbers are divisible by 2; that's why they're called even numbers! Even numbers always have either one of these digits in the ones' column: 0,2,4,6, or 8. Odd numbers always have either one of these digits in the ones' column: 1,3,5,7, or 9. An even number of objects can always be evenly divided between 2 people, but it's not so simple with odd numbers; to divide an odd number of objects between 2 people, 1 of the objects will have to be cut in half! The half of an even number is always an integer(or whole number), but half of an odd number is an integer plus ½. A special even number, zero, is its own half! Non-integers have halves, too, but only integers count as even or odd numbers.

Rational vs. Irrational

When it comes to decimals, both rational & irrational numbers can have an infinite amount of digits after the decimal point! If the digits repeat, then it's called a recurring decimal. All recurring decimals are rational because they can be written as fractions. Any rational number can be written as a fraction, including integers; all integers are quotients to 2 other integers. (For example 8/2 = 4) But not irrational numbers; although they have an infinite amount of digits after the decimal point, there are no repeating patterns, so it's difficult to guess which digit is supposed to come next. Why don't you check out the interactive Flash cartoon below this paragraph? You should already know that rational numbers can also have a finite amount of digits after the decimal point, but irrational ones always have an infinite amount!

There's an interactive Flash animation on this Web page! Click here if you don't have Flash software.

Triangular Numbers

These numbers are sums of consecutive integers starting with the number 1. The image of the 6 Annie Sisters should give you a clue why these numbers are triangular! 0 & 1 count as triangular numbers because you can have 1 object that is shaped like a triangle and...well it's that simple! As for 0, a triangular box or space can be empty, but of course you still have a triangle. Super smart scientists usually use a Greek letter to write down summation formulas. It's called the sigma and it looks like the capital letter M rotated 90 degrees counterclockwise or like a pointy version of the capital letter E. (Have you ever seen one?) Anyway, the rule is that every proceeding row must have 1 more object(or character in the image's case) than the previous row; that's how the triangle is formed!

Square/Cube Numbers

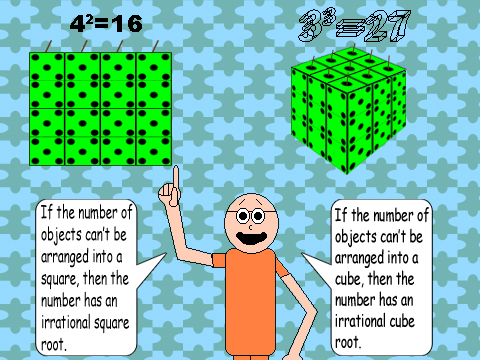When you have a square number of equal-sized objects, you can arrange them evenly into rows & columns, just like composite numbers, and the number of rows & columns will be the exact same number! For example, 16 diceberries can be arranged into 4 rows & 4 columns, with 4 diceberries in each row & column! This proves that 4 is the square root of 16. The cube is the 3-dimensional version of the square. With cube numbers, objects(remember that they must be equal in size) can be arranged & stacked evenly into a box with the cubic root of the number in each row, column, and...let's call it a level. In respect to the image, since 3 is the cubic root of 27, 27 diceberries can be stacked & arranged into a cube with 3 diceberries in each row, column, & level! The cube has 3 floors; each floor has 9 diceberries! Because 9 is 3 squared. You can also form boxes with a composite number of objects if you think 3-dimensionally! All square & cube numbers are composite! (Expect that 0 & 1 don't count as composite numbers.) If you tried forming a box with a prime number of objects, you would get an odd-looking, 3-dimensional shape!

By the way, a number can be both a square & a cube, like the number one million! The square root of 1,000,000 is 1,000. The cubic root of 1,000,000 is 100.

Back to Index Page Back to Math Trick Menu