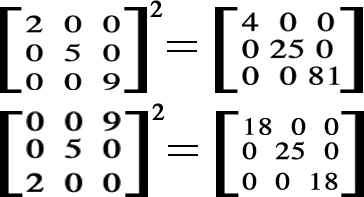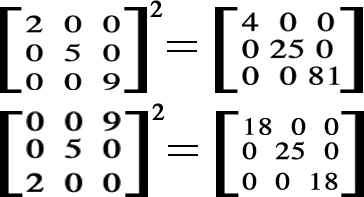Matrix Magic 2: Squaring Square Matrices with Special Diagonals
When you square square matrices with non-zero numbers on the diagonals & zeroes on the non-diagonals, the numbers on the diagonals will simply be squared!
Examples:
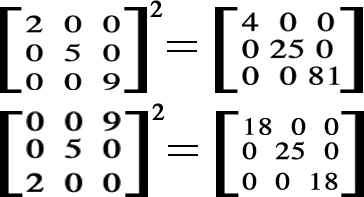

By diagonals, I mean from the top-left to the bottom-right, because according to the 2nd square matrix, if you have vice versa, well, you'll get an interesting palindrome on the diagonal as the product! However, you won't get the squares of the numbers on the bottom-left-to-top-right diagonal!
This math trick is still neat either way; in fact, it doesn't matter which kind of real numbers you put on the diagonals!
P.S.: When a square matrix has a 1 in each diagonal cell(top-left to bottom-right) & zeroes in all of the other cells, then it's an identity matrix. All identity matrices are square.
Back to Index Page Back to Math Trick Menu
© Derek Cumberbatch