Weird but interesting stuff happens when you apply infinity to certain physical things! In fact, recurring decimals are also the sums of an infinite series of fractions with a common ratio that's less than the absolute value of 1. They can even add up to a whole number! For example, 0.99999... = 1. (The 9's behind the decimal point expand forever. If they don't expand forever, then the number is not equal to 1 but a little less than 1! Remember that infinity expands forever because it's boundless; to toggle it off, simply add something to end the expansion.)

If the common ratio is greater than or equal to 1, then the infinite series won't have a sum! Because 1 + 1 + 1 + 1 + ... = ∞! In other words, adding 1 to a sum repeatedly forever will just make the sum bigger & bigger & bigger...it'll keep growing because there is no limit! (The same thing happens if you repeatedly add a number that's greater than 1, except that it'll grow at a faster rate!) For a limit to exist, the common ratio must be less than 1. Not all infinite series have a common ratio, but most of them do.
The pattern of digits to the right of the decimal point is the clue to which power of 10 to divide the respective whole number by. For example, 0.123123123... = 123/103 + 123/106 + 123/109 + ... The respective whole number in this recurring decimal pattern is 123. The 1st power of 10 in this series is 3 since there are 3 digits in that whole number; the power gets multiplied by 2 in the 2nd term, multiplied by 3 in the 3rd term, etc. The common ratio here is 1/1,000. (Or 10-3 = 1/103)
(This is how it looks in summation form:)
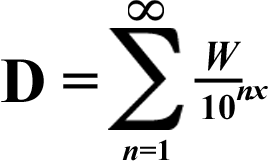
(The variable n had to be added to represent that x gets multiplied by every integer from 1 to ∞.)
What you seen above this paragraph is what happens when you apply infinity to fractions with a common ratio! However, there are many different types of infinity! As a bonus for viewing this Web page, here's another type of infinity to see below!
There's an interactive Flash animation on this Web page! Click here if you don't have Flash software.
An infinite series of ladies followed by a man would NEVER have a man in it because it simply doesn't end! If you keep adding ladies to a series forever, then you can never have a man in it...Until you stop expanding it with just ladies & add a man for a change, which breaks the infinitude of ladies! So with infinity toggled on, "Ladies First" converges to "Ladies Only"! (It has the same effect as a girls-only club in the real world.)
The term first isn't exclusionary, but the term only is! In other words, "Ladies First" doesn't exclude gentlemen; it just means: "Let the ladies go first"; but "Ladies Only" means: "Let nobody but ladies get in!" which DOES exclude gentlemen! If a series of ladies is infinite, then you can't ask: "What if it ends with a man?" because there is no end; otherwise, the series would not be infinite. Furthermore, it's technically impossible to get to infinity; not even the great googolplex is close to infinity! You could eventually reach the googolplex if you tried. (But it'll take a very, very long time if you start at 1, going up 1 integer per second!) All numbers, no matter how big they are, are finite. But infinity is not finite! In fact, infinity is not a number at all, it is an idea, a concept, something that never ends. The only way to get to infinity is to never ever stop!
Back to Index Page Back to Math Trick Menu
© Derek Cumberbatch