Pythagorean Power: Exponential Excellence

This math trick is like an extended version of the Pythagorean Theorem!

The examples below show why!

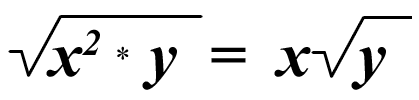
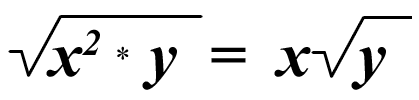
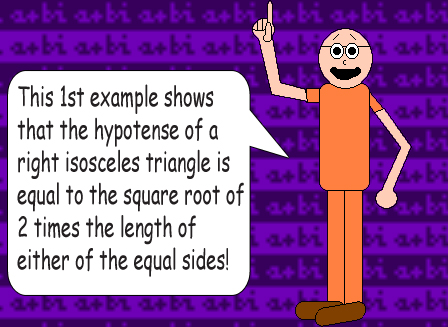
(x^2 + x^2)^½ = (2x^2)^½ = x * (2)^½ or x * 1.4142...

(That irrational number is the square root of 2)

The caret (^) is the symbol of exponentiation. Raising a number to the power of ½ gives you the square root.

What number is x equal to in all these examples? Any number you want it to be!

(x^2 + x^2 + x^2)^½ = (3x^2)^½ = x * (3)^½ or x * 1.7320...

(That irrational number is the square root of 3)

(x^2 + x^2 + x^2 + x^2)^½ = (4x^2)^½ = x * (4)^½ or 2x

(4 has another integer for a square root, which is 2)

(x^2 + x^2 + x^2 + x^2 + x^2)^½ = (5x^2)^½ = x * (5)^½ or x * 2.2360...

(That irrational number is the square root of 5)

If y has a rational square root, then x will be multiplied by a rational number!

Remember that multiplication is actually glorified addition. In the function on top of this page, the variable y tells you how many times you should add x (or rather its square) to itself. In other words, if y = 7, then x is multiplied by 7 so you get x + x + x + x + x + x + x = 7x. Exponentiation is glorified multiplication. (x * x * x = x^3) In algebra, exponentiation is usually done before multiplication, which is usually done before addition; higher calculation levels are done before lower ones. However, parentheses tell us to do the math between them first before doing any math on the outside!

Addition & subtraction are on the same level; the lowest level of calculation. The next higher level is multiplication & division; then exponentiation, radicals & logarithms, which is the highest. This is called the "Please Excuse My Dear Aunt Sally" Rule.

Although this trick works with all numbers, it's much more interesting with integers!

Back to Index Page Back to Math Trick Menu