Super Summation 4

Because of this fact Brain just mentioned, in the summation formula above, whatever integer you pick to be x above the sigma(or summation sign), the sum will always add up to x!

Example:

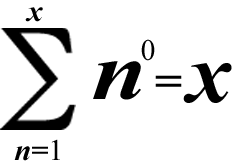
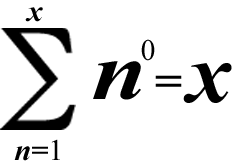
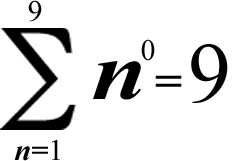
1^0 + 2^0 + 3^0 + 4^0 + 5^0 + 6^0 + 7^0 + 8^0 + 9^0 = 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 1 × 9 = 9

(1 is the number of multiplicative identity, so n × 1 = n; notice that there are 9 1's!)

The caret (^) is the symbol of exponentiation. Raising a non-zero number to the power of zero(0) always gives you 1.

You can only pick counting numbers to be x in this summation formula because 1 is the number below the sigma, to the right of the small n & equal sign. All positive integers are counting numbers. (By the way, zero(0) isn't a counting number because it's neither positive nor negative; it's neutral)

Back to Index Page Back to Math Trick Menu