Cuckoo For Conjugates!

When you divide a complex number by its conjugate, the absolute value of the quotient is always equal to 1!

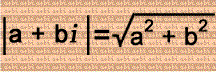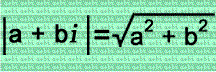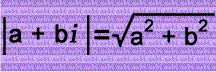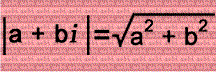
Remember that this is the formula for the absolute value of a complex number:

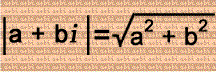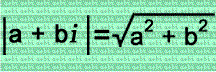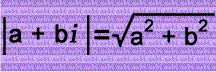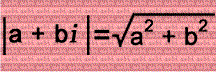
The absolute value of a + bi = the square root of the sum of a^2 and b^2

Examples:

(1 + i) ÷ (1 - i) = i

(1 - i) ÷ (1 + i) = -i

|i| = 1; |-i| = 1

Obviously, the absolute value of i is 1; multiplying i by any real number just multiplies the absolute value, so |xi| = |x|. (Don't forget that absolute value is always positive!)

(2 + 3i) ÷ (2 - 3i) = -5/13 + 12/13i

(2 - 3i) ÷ (2 + 3i) = -5/13 - 12/13i

|-5/13 + 12/13i| = 1; |-5/13 - 12/13i| = 1

It doesn't matter if the real or imaginary parts of the complex numbers are rational or not, the quotient's absolute value will always be 1 as long as the divisor & dividend are conjugates! Remember that the conjugate of a + bi is a - bi.

(3/2 + i/3) ÷ (3/2 - i/3) = 77/85 + 36/85i

(3/2 - i/3) ÷ (3/2 + i/3) = 77/85 - 36/85i

|77/85 + 36/85i| = 1; |77/85 - 36/85i| = 1

Note: If the imaginary part is a fraction, you can put i in the numerator, especially if it's a unit fraction.

Since their absolute value equals 1, the quotients are reciprocals of each other! The only difference is the sign between the real & imaginary parts! In other words, if a complex number has an absolute value of 1, then its reciprocal is its conjugate!

Notice how some of the pluses change to minuses & vice versa!

I thought about using irrational numbers in this final example, but it made things too complicated! So I used fractions instead!

(-3/2 + 5/6i) ÷ (-3/2 - 5/6i) = 28/53 - 45/53i

(-3/2 - 5/6i) ÷ (-3/2 + 5/6i) = 28/53 + 45/53i

|28/53 - 45/53i| = 1; |28/53 + 45/53i| = 1

Conjugates share the same absolute value!

Back to Index Page Back to Math Trick Menu