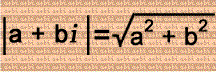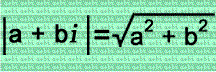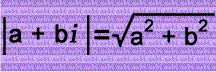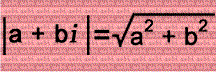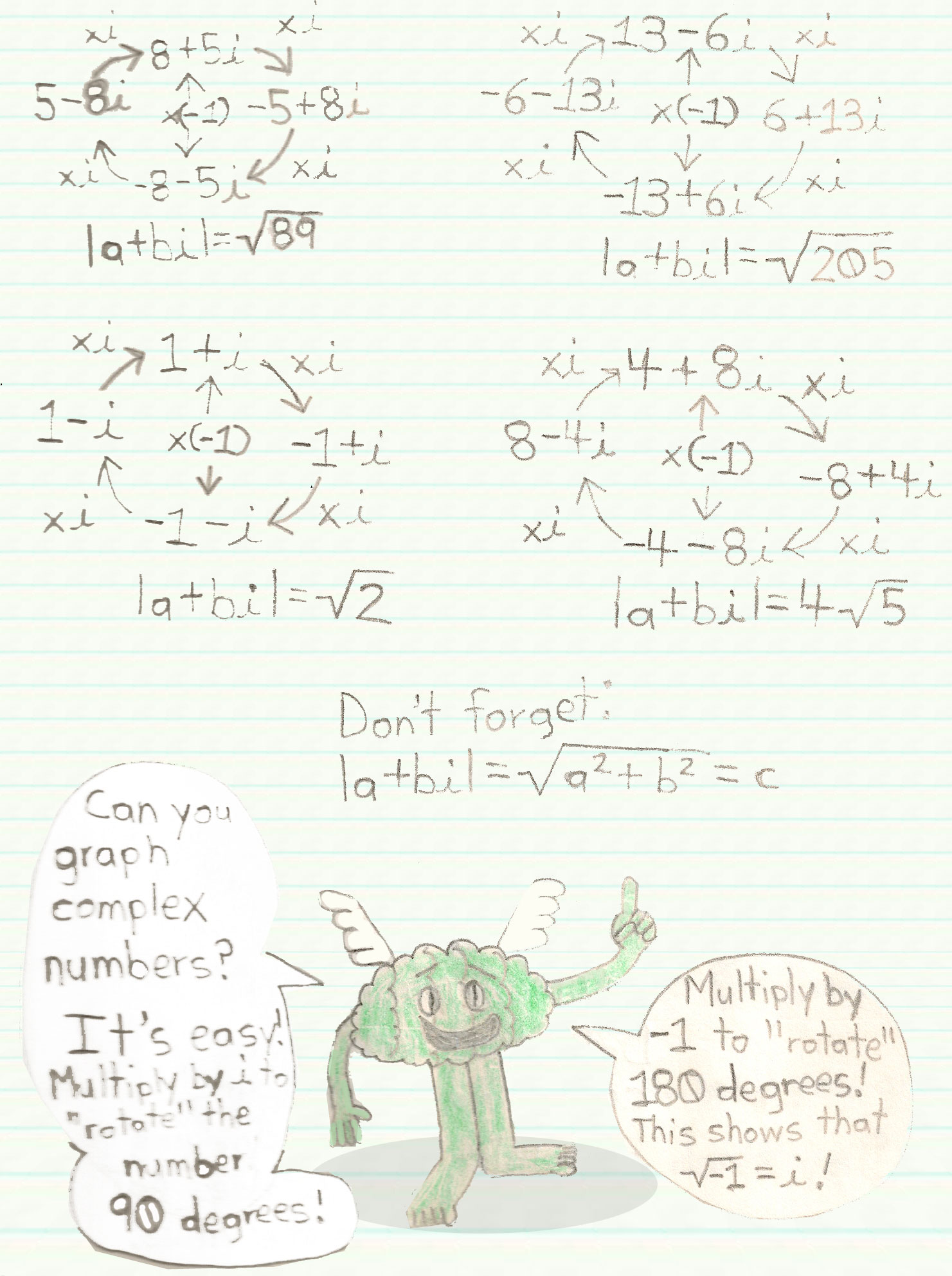Complex Numbers Meet the Pythagorean Theorem
Here is one way imaginary numbers relate to the real world.
What does this have to do with imaginary numbers? The absolute value of a complex number:
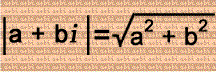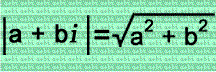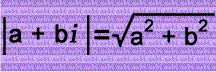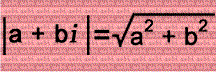
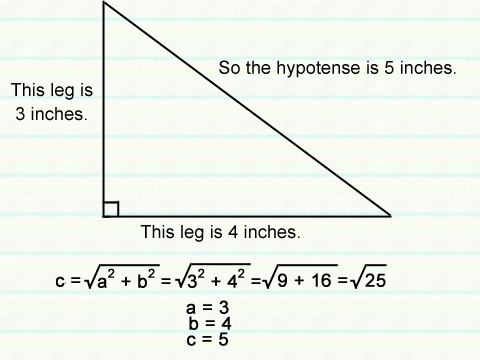
It's similar to the Pythagorean Theorem! In the complex number, a & b represent the triangle's legs, and the absolute value of the complex number represents the hypotense! There are 8 possible complex numbers for the triangle.
3+4i, -4+3i, -3-4i, 4-3i, 3-4i, -3+4i, -4-3i, 4+3i
You can have the legs of a right triangle swap values without changing the length of the hypotense!
Multiply by i to get to the next complex number! The cycle will keep going and going and going...By the way, these complex numbers have the same absolute value! This trick will work on any complex number!
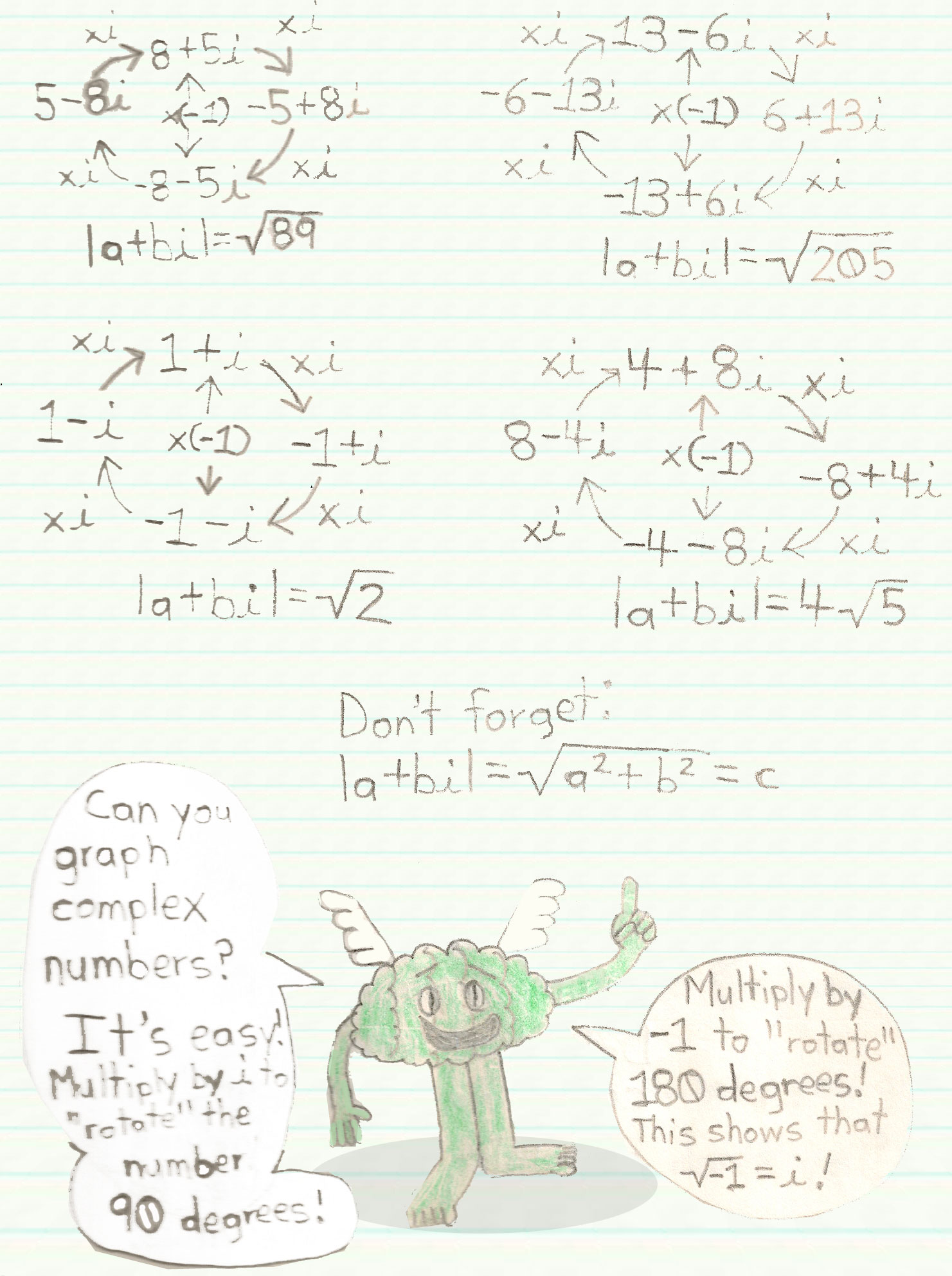

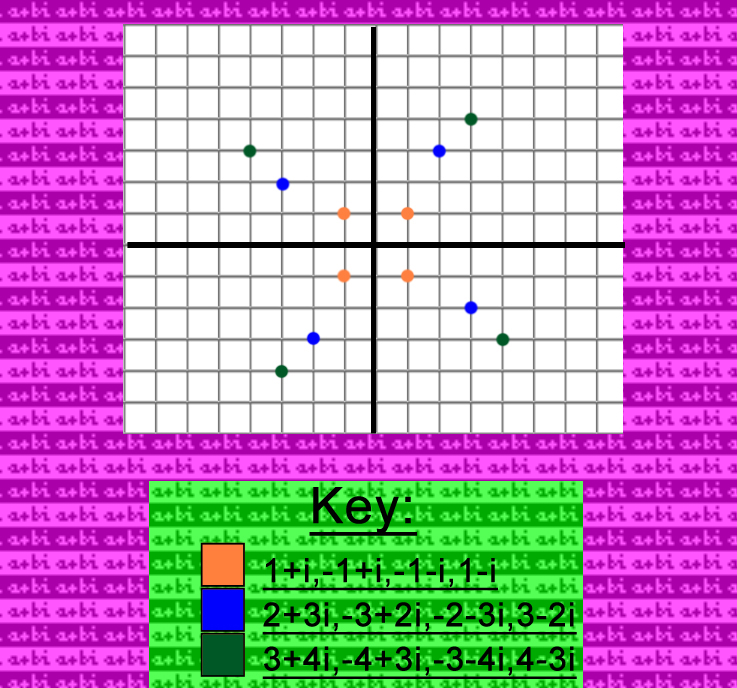
This is a graph of complex numbers. Dots that match in color have the same absolute value. Multipying or dividing by i or -1 does not change the absolute value! One last thing: If you multiply or divide by i 4 times in a row, or by -1 twice, then you go back to your original complex number!

Back to Index Page Back to Math Trick Menu
© Derek Cumberbatch