Complex Number Kookiness 3: Dotted Distance

When you subtract 2 complex numbers, the absolute value of their difference tells you how far apart they are. Shown below is how you subtract complex numbers:

|(a + bi) - (c + di)| = |(a - c) + (b - d)i|

The absolute value of a complex number:

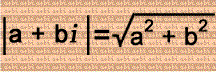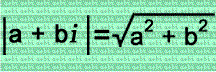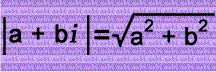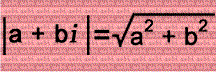
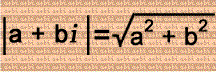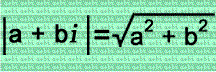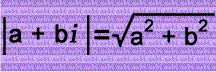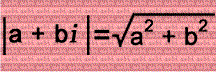
The absolute value of a + bi = the square root of the sum of a^2 and b^2

Examples:

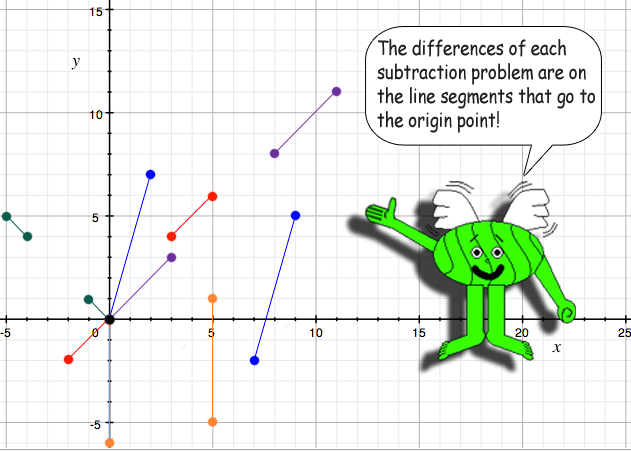
|(3 + 4i) - (5 + 6i)| = |-2 - 2i| = 2√(2) or √(8)

|(9 + 5i) - (7 - 2i)| = |2 + 7i| = √(53)

|(11 + 11i) - (8 + 8i)| = |3 + 3i| = 3√(2) or √(18)

|(5 - 5i) - (5 + i)| = |-6i| = 6

|(-5 + 5i) - (-4 + 4i)| = |-1 + i| = √(2)

Note: Considering a + bi, if you see a minus sign instead of a plus sign between a & b, then b is negative; similarly, if you see a minus sign before a, then a is negative. In other words, -1 × (a + bi) = -a - bi.

Below is a plotted graph of every complex number used in the examples: (Each example has a different color; line segments in the same color are equal in length!)

This math trick shows another way that imaginary/complex numbers can be useful in the real world!

Back to Index Page Back to Math Trick Menu