Mega Matrix Multiplication 2

If you multiply a single row matrix by a single column matrix with the same number in each cell, then something quite interesting happens!

Let's call the single row matrix Matrix A & the single column matrix Matrix B. If you multiply Matrix A by Matrix B, then you get a single cell matrix with the square of the cells' number multiplied by the number of rows in Matrix B & the number of columns in Matrix A! (Which are the same number)

y = zx²

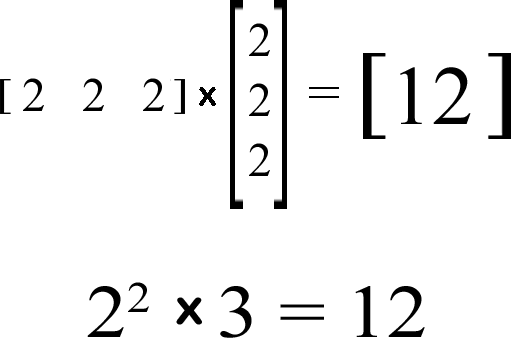
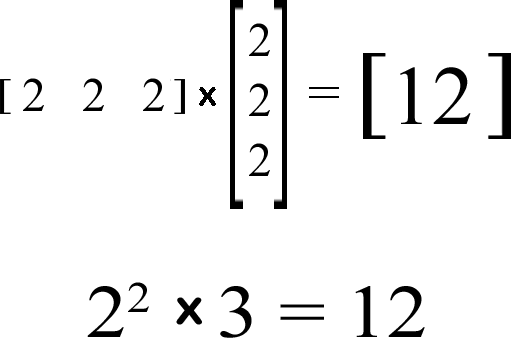
x = the number in each matrix cell

y = z multiplied by the square of the number in each matrix cell

z = the number of rows in the 2nd matrix & columns in the 1st matrix

Y is the number you'll get in the cell of the equation matrix!

Note: This is the same function seen in Math Trick #12: "Squaring Square Matrices". It happens to be coincidental to this one.

There are special rules to multiplying matrices. Here are 2 examples:

The number of columns in the 1st matrix must match the number of rows in the 2nd matrix.
The matrix in the product will have the same number of rows as the 1st matrix & the same number of columns as the 2nd matrix.

Multiplication is commutative with ordinary numbers, but not with matrices because of the way they have to be multiplied...(Do you know how to multiply them? Because of how tricky it is, you'll want to use a calculator!)

Just so you know, if you multiply Matrix B by Matrix A, you would get a square matrix with the square of the number in each cell.

All single-celled matrices are their own transpositions!

Here's another example with fractions:

The fractions make the logic of the function look more obvious! This will work with irrational numbers, too!

You can use any real number you want in this math trick, but remember that you must put the same number in each matrix cell!

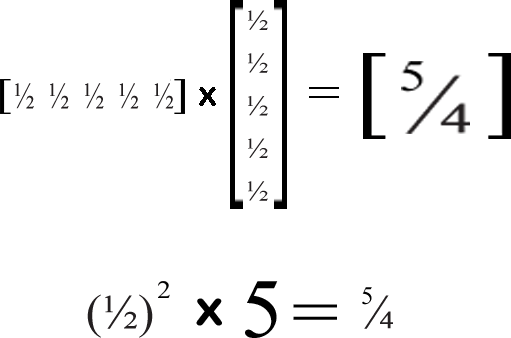
Back to Index Page Back to Math Trick Menu