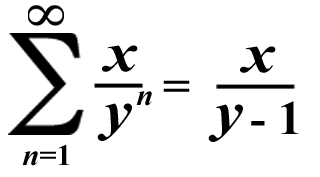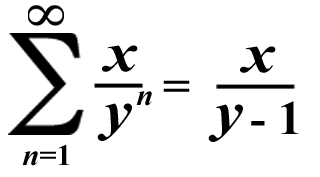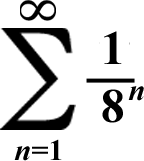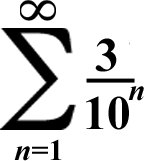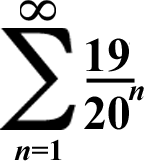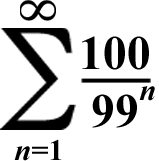Super Summation
Some infinite series have sums; some don't. For an infinite geometric series to have a sum, its common ratio must be less than the absolute value of 1. A specific formula can be used to determine the sum of the infinite series. If an algebraic fraction is used, then...
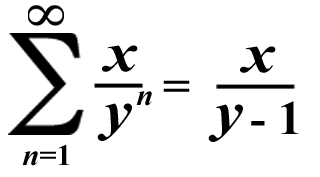
Examples:
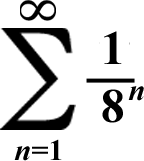
First Term: 1/8
Common Ratio: 1/8
(1/8)/(1 - 1/8) = 1/7
(...And 8 - 1 = 7)
The common ratio is the next term divided by the previous term.

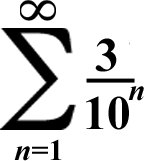
First Term: 3/10
Common Ratio: 1/10
(3/10)/(1 - 1/10) = 3/9 = 1/3
(...And 10 - 1 = 9)
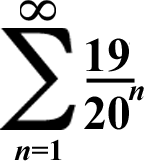
First Term: 19/20
Common Ratio: 1/20
(19/20)/(1 - 1/20) = 19/19 = 1
(...And 20 - 1 = 19)
The Final Example:
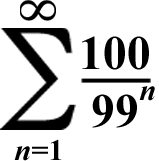
This time, the numerator of the algebraic fraction is greater than the denominator!
First Term: 100/99(or 1 + 1/99)
Common Ratio: 1/99
(100/99)/(1 - 1/99) = 100/98 = 50/49(or 1 + 1/49)
(...And 99 - 1 = 98)
One last thing: If the common ratio is greater than, or equal to the absolute value of 1, then the infinite series has no sum, because in that special formula that Dr. John Von Foolish showed you, you would have to divide by zero, which gives you infinity! You could also get a negative number for an answer, which wouldn't be the truth!
Back to Index Page Back to Math Trick Menu
© Derek Cumberbatch