Lovely Logarithms!

Here's a function:

y = log_x(2x)

If x is equal to a power of ½, then y = (n - 1)/n! (n is the exponent that you raise x by)

Note: n ≠ 0 because division by zero(0) is undefined.

Brain saying "WOW!"

x	y
1/2	0
1/4	1/2
1/8	2/3
1/16	3/4
1/32	4/5
1/64	5/6
1/128	6/7
1/256	7/8
1/512	8/9
1/1024	9/10
½^n	(n - 1)/n

Since ½ is the reciprocal of 2, the negative powers of ½ are the positive powers of 2 & vice versa!

If x is equal to a power of 2, then y = (n + 1)/n!

Note: Again, n ≠ 0 because division by zero(0) is undefined.

x	y
2	2
4	3/2
8	4/3
16	5/4
32	6/5
64	7/6
128	8/7
256	9/8
512	10/9
1024	11/10
2^n	(n + 1)/n

Also, remember this fact about fractions & mixed numbers:

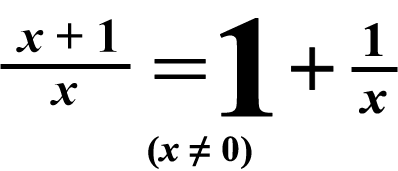
You can also see this fact on the Main Page of the Math Section.

Technically, 1 is the zeroth power of 2 & also the zeroth power of ½, but if x = 1, then y is undefined because log₁T is indeterminate. When the number 1 is the base of a logarithm, it's like dividing by zero(0)! Besides, 1^T = 1, every time!

Also, notice how I didn't use the exclamation mark as the factorial function!

Back to Index Page Back to Math Trick Menu

© Derek Cumberbatch