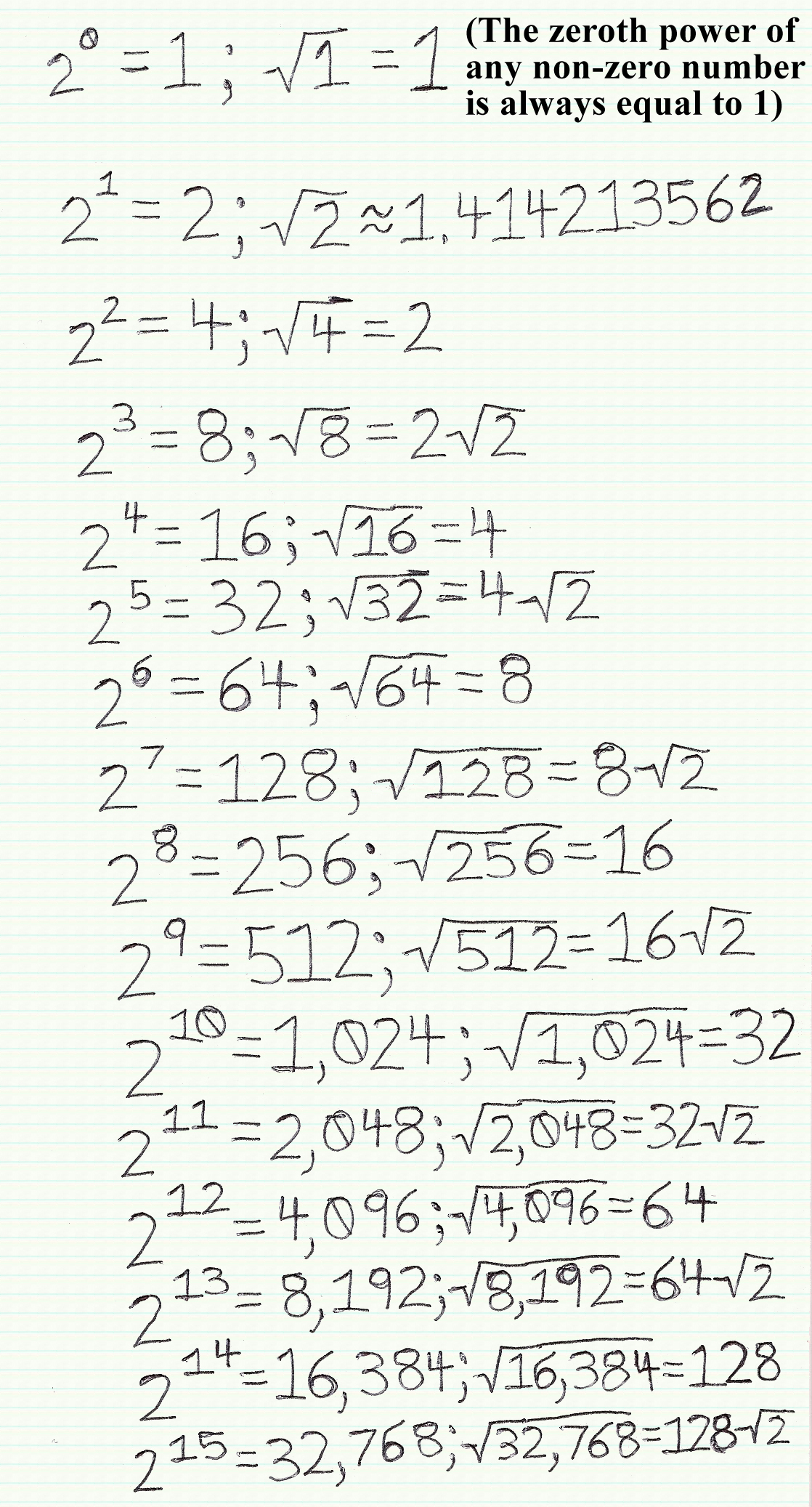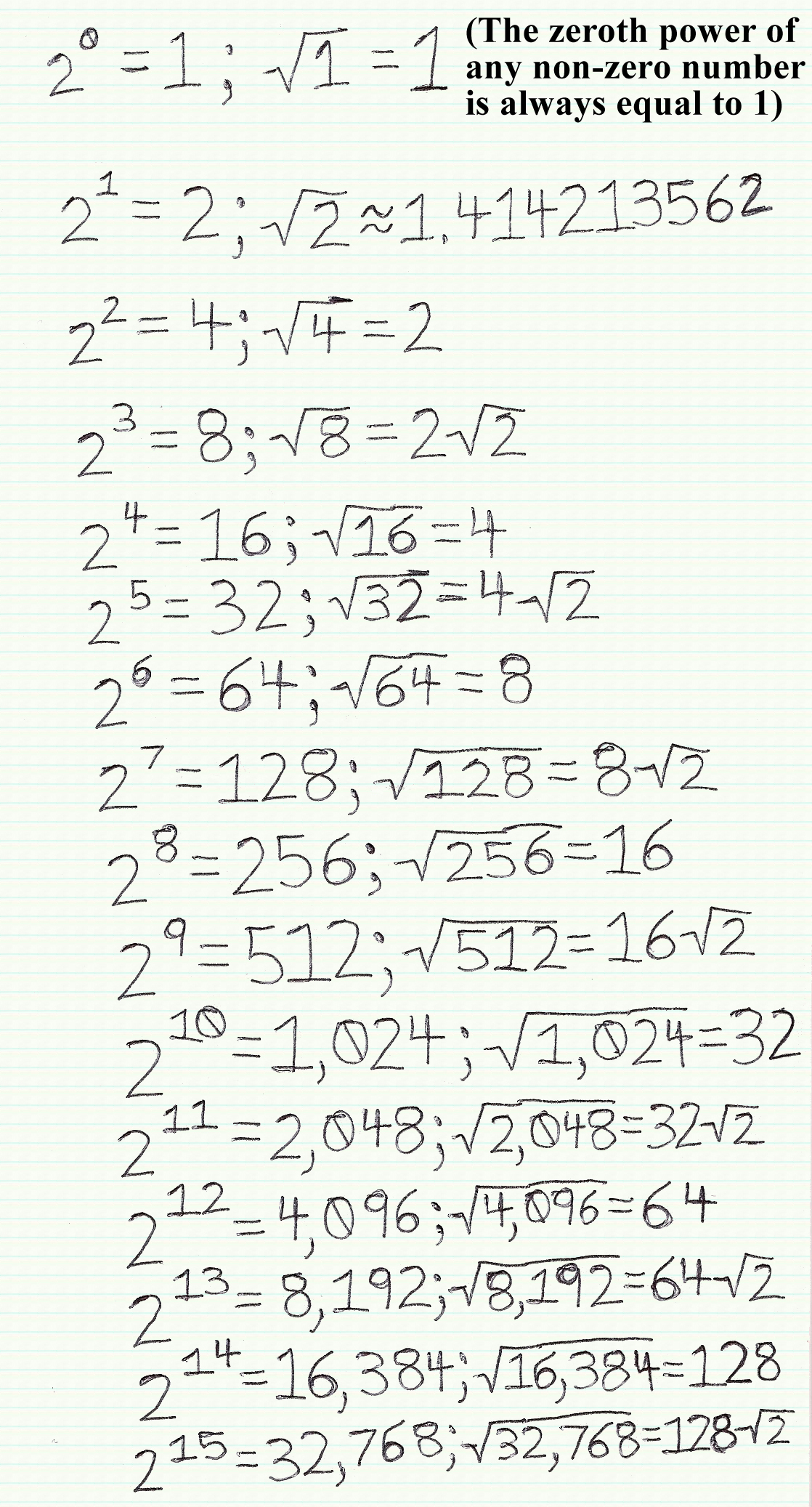The Square Roots of the Powers of 2

There's something special about the square roots of the powers of 2, if you look closely...

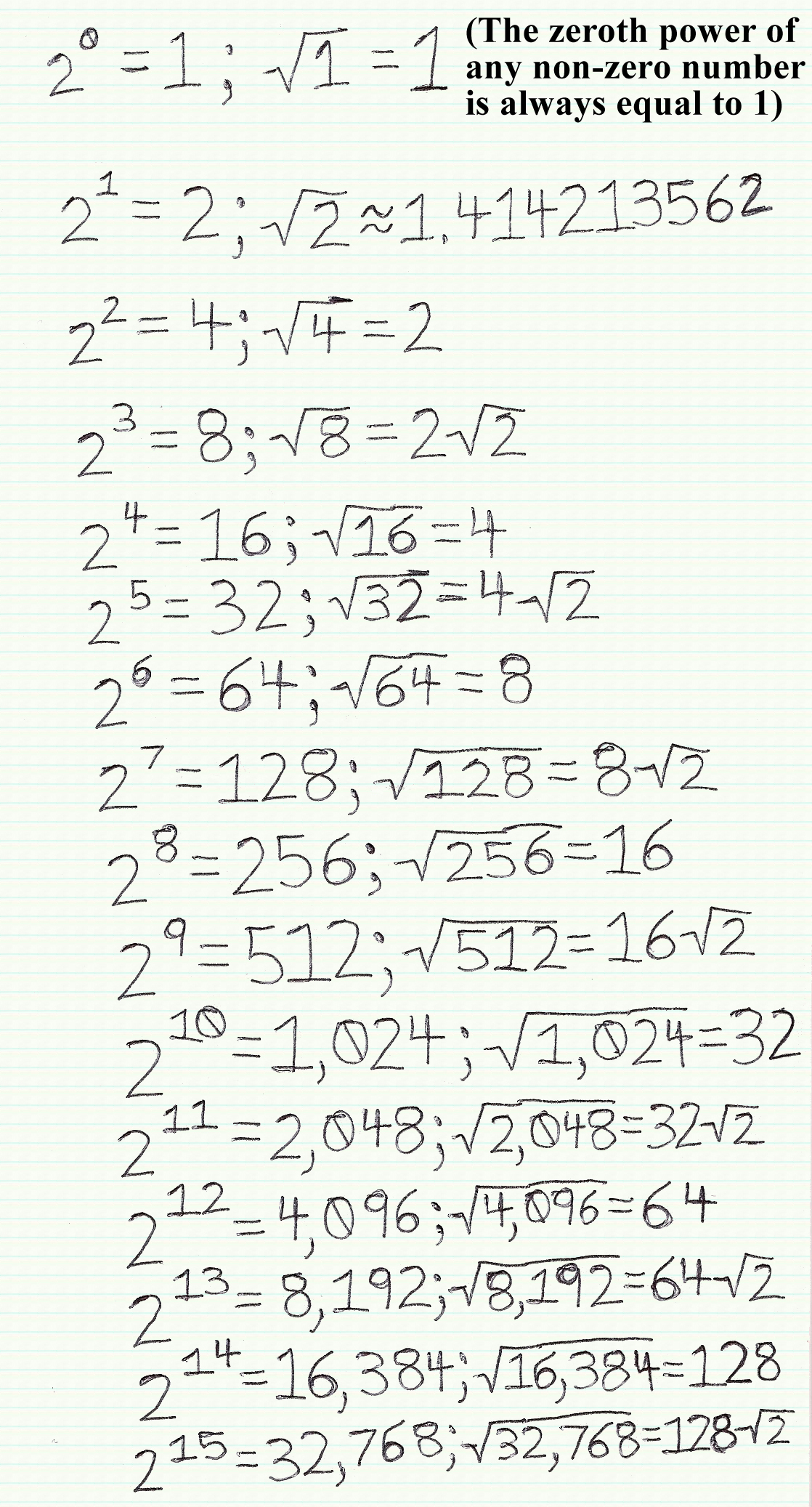
Have you noticed what's special about the square roots when 2 is raised to an odd exponent? When 2 is raised to an even exponent, the square root of the power is equal to 2 to the power of the exponent's half! But when 2 is raised to an odd exponent, the square root of the power is equal to a multiple of the square root of 2! In fact, it'll be 2 to the half of the previous even exponent multiplied by the square root of 2!

Another important fact to remember about square roots is that:

X^½ = the square root of X

The caret (^) is the symbol of exponentiation. Raising a number to the power of ½ gives you the square root.

What if you raise 2 to a negative exponent, you ask? Simple! That'll just give you the reciprocals of the positive powers!

P.S.: Raising 2 to the power of an imaginary or complex number will give you a random complex number & the square roots of such numbers are also complex. So this math trick will only work with real numbers. Pick real integers as exponents only. And remember: 2 must be the base!

Back to Index Page Back to Math Trick Menu