Powerful Patterns 4: Summation Fractions

Look at the summations below. You should notice a pattern...

The fractions have consecutive integers as numerators & denominators, but the denominators are less than the numerators by 1! There's a formula for this unique summation pattern:

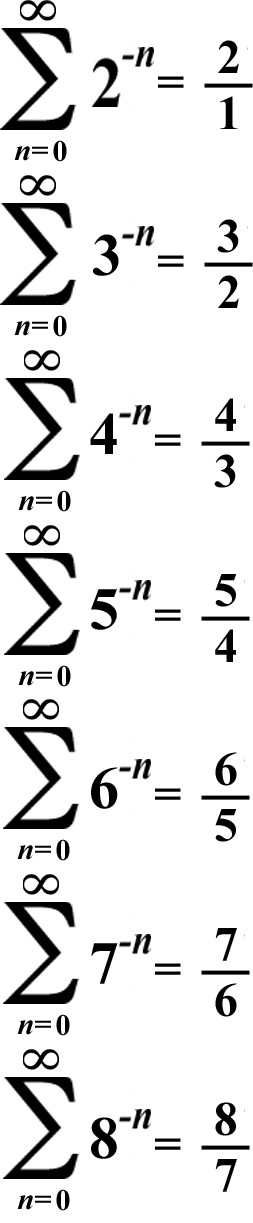
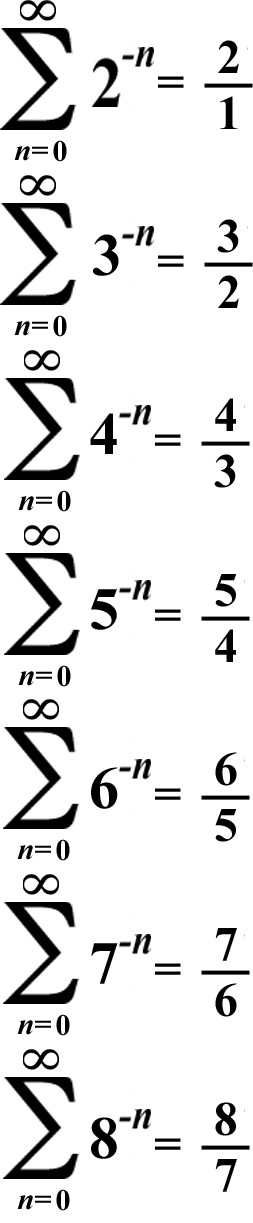
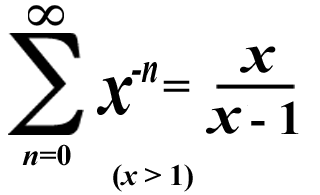
By the way, I printed the fractions in the summations above as improper fractions to make them easier to read. When the numerator is equal to the denominator + 1, the fraction can also be printed as a mixed number that's equal to 1 + 1/(the denominator).

Since 1 is the number of multiplicative identity, dividing by it gives you the dividend as the quotient & all integers are multiples of 1! If 1 is the denominator, then the fraction is an integer! (Algebraic fractions don't count; an algebraic fraction is a fraction that has a non-integer for a numerator or denominator.)

Speaking of patterns, maybe you already seen some other numerical math patterns that other mathematicians already discovered & published! (Besides me or you; any open-minded person can be a great mathematician, like me!)

Back to Index Page Back to Math Trick Menu