Delightful Division 2: Number of Nines in a Divisor

You can easily get recurring decimals as a quotient when you have a divisor with only nines as the digits!

Examples:

1/9 = 0.1111111111...

1/99 = 0.01010101...

1/999 = 0.001001001...

1/9,999 = 0.000100010001...

1/99,999 = 0.0000100001...

Have you noticed the pattern yet? The more nines the divisor has, the more zeroes you're likely to get in the quotient to the right of the decimal point! Don't forget that recurring decimals go on forever; they have an infinite amount of digits behind the decimal point!

More Examples:

This time, the dividend is random.

3/9 = 0.3333333333... (Which is the same as 1/3)

17/99 = 0.1717171717...

123/999 = 0.123123123... (Which is the same as 41/333)

78/9,999 = 0.007800780078... (Which is the same as 26/3,333)

25/999 = 0.025025025...

3/999,999 = 0.000003000003... (Which is the same as 1/333,333)

625/999,999,999 = 0.000000625000000625...

If you don't want any zeroes in your quotient, pick a dividend (without any zeroes) that has as many digits as the divisor. You will, however, always get these digit patterns that repeat over & over forever!

Oops! I almost forgot something! Sometimes, people don't bother printing the integer zero to the left of the decimal point if the decimal is less than 1 but greater than 0, so [0.x] = [.x]!

Ever wonder why 0.999999999... = 1? This final example will show why!

Final Example:

9/9 = 99/99 = 999/999 = 9,999/9,999 = et cetera = 0.999999999... = 1

(Dividing any non-zero number by itself always gives you 1 as the quotient!)

Remember this summation formula from "Super Summation"? If x = 9 & y = 10, then the infinite geometric series has a sum which is equal to 1 because the common ratio of the terms is 1/10. Furthermore, each term is equal to 9/10^n. (9 is divided by each consecutive power of 10 to infinity onward. That gives 9/10 + 9/100 + 9/1,000 + ... = 0.999999999999... There's an infinite amount of nines behind the decimal point!)

Since the common ratio is 1/10 which is less than the absolute value of 1, you have to subtract that from 1 to get 9/10, & then divide that by the 1st term of the infinite geometric series, & BINGO! You get 1 since the 1st term is also 9/10. (You can see the formula for the sum of an infinite geometric series on the "Super Summation" Page!)

Brain said this somewhere on the "Super Summation" Page, but he's here to say it again anyway to remind you:

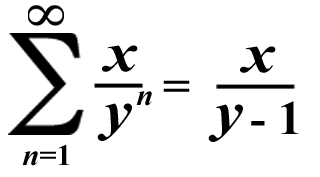
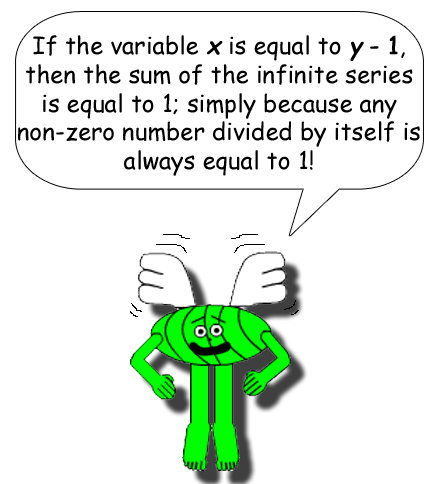
Back to Index Page Back to Math Trick Menu