The Irrational Number Phi

This number is also known as the Golden Ratio. It's approximately equal to 1.618 and it is written as a Greek letter, just like Pi.

Phi looks like this: φ

Pi looks like this: π

In fact, they're both Greek letters, but this page is about the irrational number Phi! What's so interesting about this number? Squaring this special number is same as adding 1 to it! 1 divided by this number or raising it to the power of -1 is the same as subtracting 1 from it!

φ + 1 = φ²

1/φ = φ^-1 = φ - 1

However, if Phi is negative...

1/-φ = (-φ)^-1 = -φ + 1

Note: Adding the square root of 5 to -φ gives you φ - 1 and subtracting the square root of 5 from φ gives you -φ + 1!

This unique number is the intersection of these 2 functions:

Y = X²

Y = X + 1

Actually, these functions intersect twice; but at each intersection, X = -φ + 1 or φ. Here's how Phi looks as an algebraic fraction:

Note: You can multiply all 3 numbers in the fraction individually by a non-zero number(the exact same multiplier for each of the 3 numbers) to get the exact same ratio!

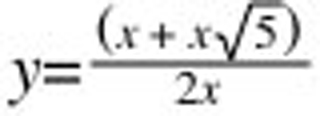
In this function, y will always be equal to φ as long as x ≠ 0!

Note: If you delete the 2 in the denominator of the function, then y will be equal to 1 + √(5), which is phi(φ) times 2!

Also:

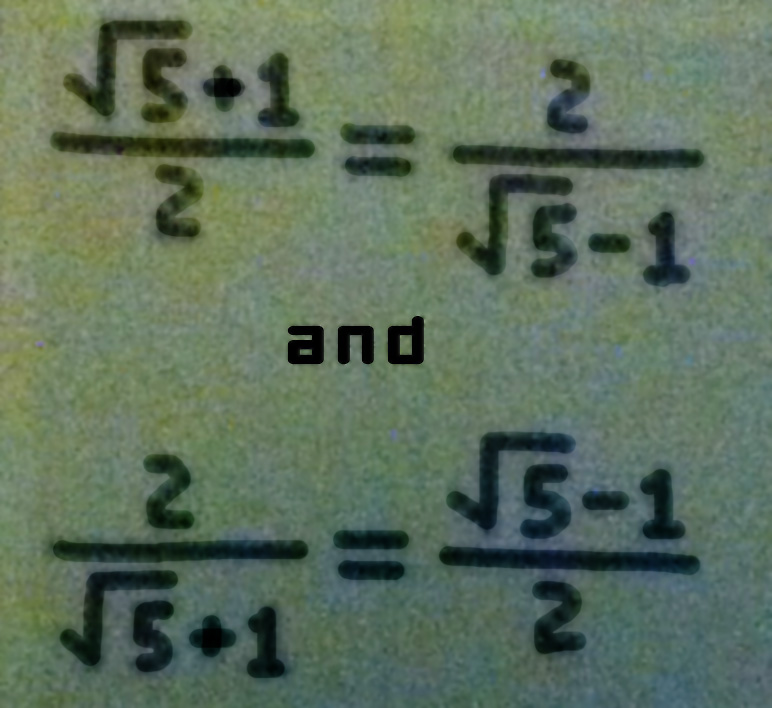
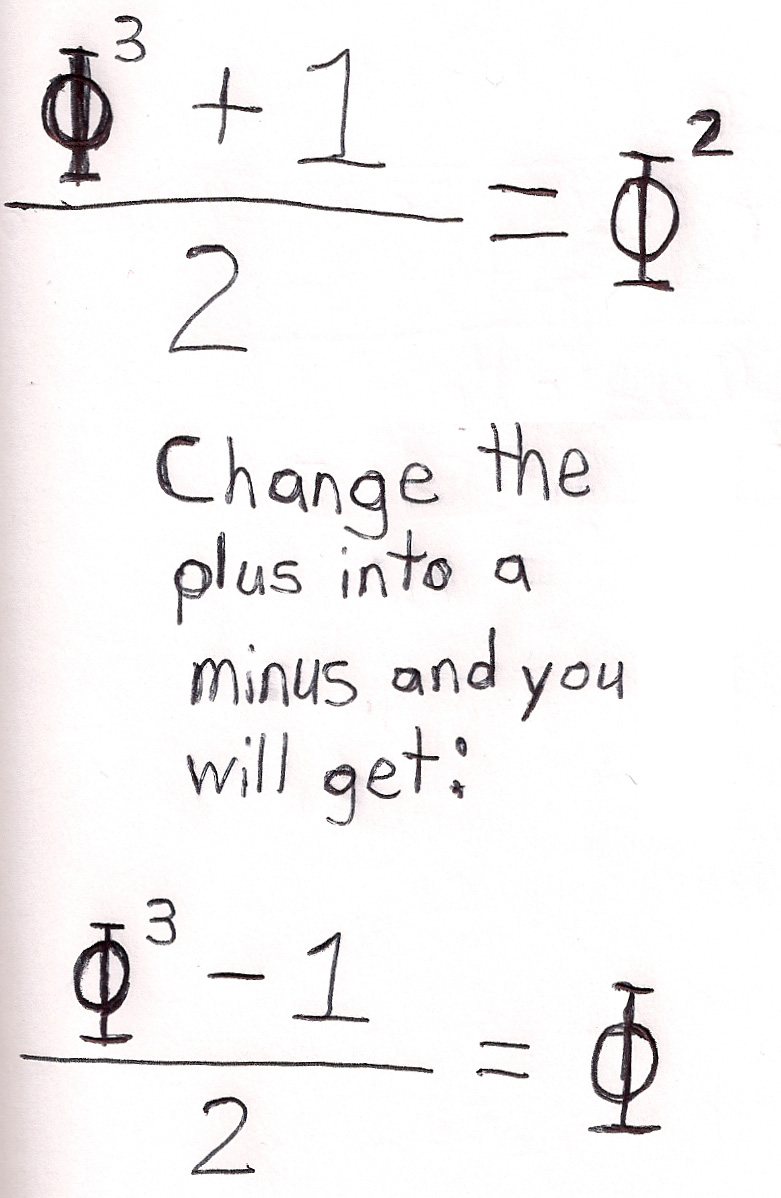
P.S.: If the numbers φ³ & 1 swap places with the minus sign in-between them, then you'll get -φ because subtracting bigger numbers from smaller numbers makes the difference negative! (φ³ > 1)

Even more information:

Note: With a minus sign between the 1 & √(5), with √(5) on the right & the 1 on the left, the algebraic fraction is equal to -φ + 1! (If it's vice versa, then the algebraic fraction is equal to φ - 1.)

Here's another fact about Phi: (φ + 1)^x = φ^2x.

One more fact about Phi: φ^x = φ^x-1 + φ^x-2. Also, φ^x = φ^x+2 - φ^x+1.

Back to Index Page Back to Math Trick Menu

© Derek Cumberbatch