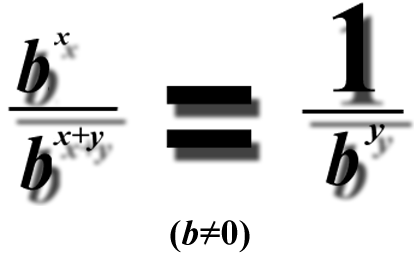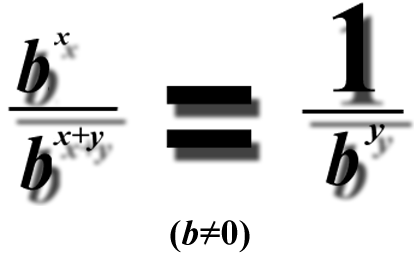Delightful Division
Here's a function with exponents in the numerator & denominator of a fraction!
b^x ÷ b^(x + y) = 1 ÷ b^y
Again, here's how the function looks as algebraic fractions:
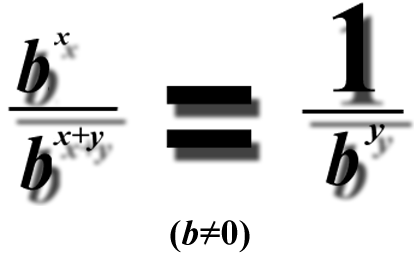
You can also say that the numerator is a dividend and the denominator is a divisor of a divison problem; in fact sometimes, fractions ARE division problems!
Examples:
b = 5, x = 2, y = 1
5^2 ÷ 5^3 = 25 ÷ 125 = 1/5
(You know 2 + 1 = 3, right?)
b = 7, x = 4, y = 3
7^4 ÷ 7^7 = 2,401 ÷ 823,543 = 1/343
(You know 4 + 3 = 7, right? Also, 343 is 7 cubed!)
b = ½, x = 8, y = 5
½^8 ÷ ½^13 = 1/256 ÷ 1/8,192 = 32
(You know 8 + 5 = 13, right? This time we got an integer as the quotient!)
If b is a fraction, then the quotient will be an integer.
b = 10, x = 92, y = 1
10^92 ÷ 10^93 = 1/10
You should get the idea by now.
Those powers of 10 are so big that I would have to type a total of 185 zeroes!

Note: Even if the variable b is a non-integer(rational or irrational), then the trick will still work out; however, if x and/or y are non-integers, something complicated happens and it's not very pretty! The trick still works, but calculations get very difficult to figure out when the exponents(x & y) are NOT integers! You get irrational quotients, etc. So I suggest you only use integers as the exponents! Finally, if you choose the variables to be negative numbers, then you'll either get a negative fraction or an integer as the quotient, depending on how many of the variables are negative.

P.S.: Don't use imaginary or complex numbers in this math trick; this trick is too tricky with them included!

Back to Index Page Back to Math Trick Menu
© Derek Cumberbatch