Miss 1's Garden of Factor Trees

What's a factor tree, you ask? Well you'll see what they are on this Web page!

A factor tree can be formed with any composite number! Some composite numbers have so many factors that several possible factor trees can be formed from them! However, perfect squares (numbers with integer square roots) are likely to have symmetrical factor trees, especially if their square roots are prime.

It seems as if 1 should be a prime number since it can be divided evenly by 1 & itself, (Plus it's the number 1 itself!) but it's neither prime nor composite; it's idempotent. By the way, the only other idempotent number is 0. (0 is the even one & 1 is the odd one)

Here's another reason why 1 is idempotent:

n = n × 1 = n × 1 × 1 = n × 1 × 1 × 1 = n × 1 × 1 × 1 × 1 = et cetera

Multiplication by 1 doesn't change the product, no matter how many times you do it! Plus, 1 to the power of any number is still 1!

There's a special rule about composite numbers: Each composite number is equal to a unique product of primes. The same prime number can be used more than once. (For example, if you have to multiply by 5 twice, it's the same as squaring it, but you still get the same composite product) Finally, all even composite numbers have the number 2 as a factor of course; 2 is the only even prime number.

Observe the factor trees below. The numbers at the forks are the composite factors of the trees' main composite numbers. The prime numbers are the fruits of these trees!

Note: Don't forget that all prime, composite & idempotent numbers are factors to themselves. (If you can't divide by zero, then can zero be a factor to itself? There's a good question...)

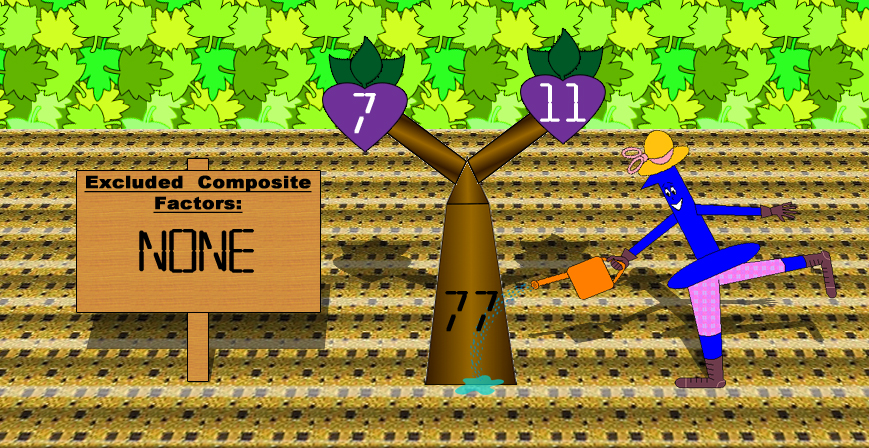
Some composite factors get excluded from the trees sometimes, but you can multiply 2 or more included factors to found out what they are. Alternatively, you can divide the main composite number by any of the factors included to find the ones excluded. However, composite numbers never have factors that are greater than their halves. The bigger the composite number is, the more factors it's likely to have! You always get to the prime factors in the end!

Back to Index Page Back to Math Trick Menu

© Derek Cumberbatch