Rad Radicals!

No matter what the variables x or z are, this statement will be true! However, the numerator of the algebraic fraction must be equal to 1.

Examples:

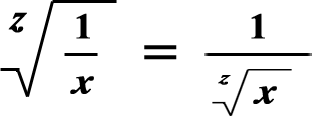
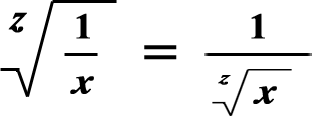
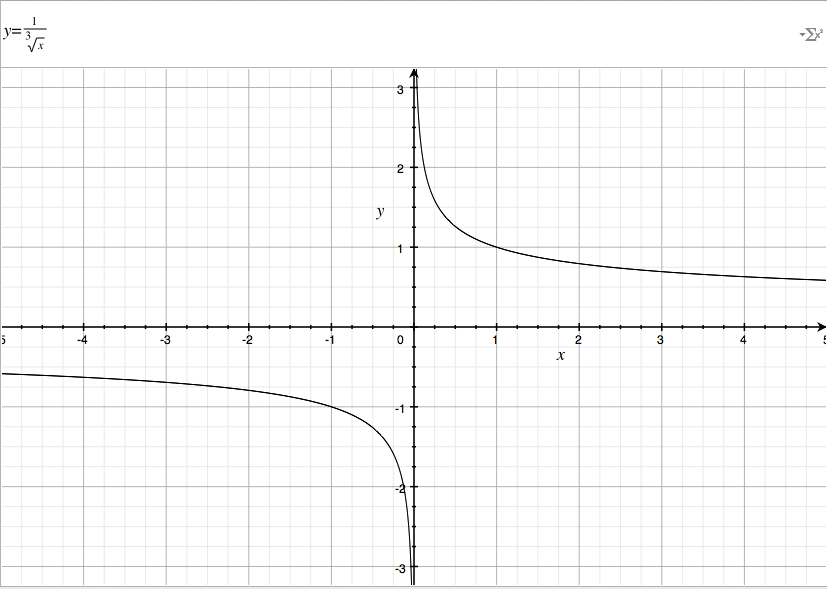
Pictured here are the functions when z = 3:

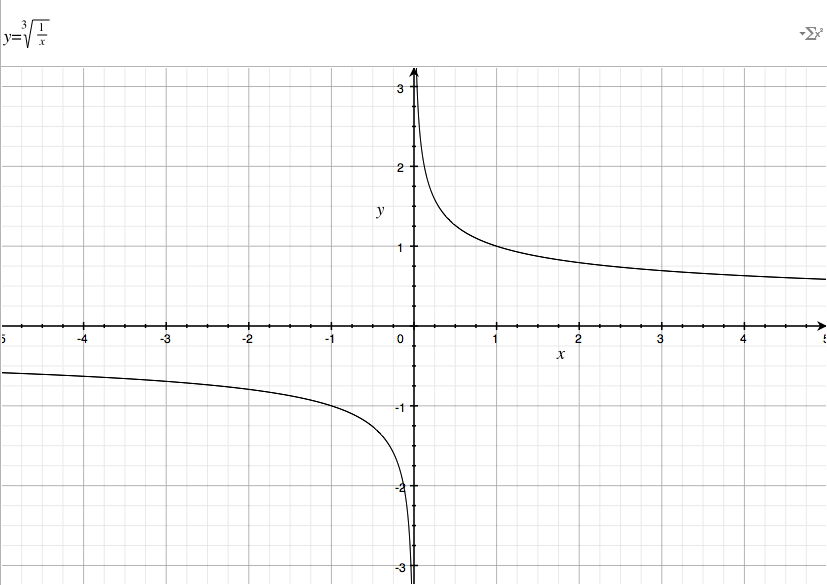
They both look exactly the same, don't they? That's because the 2 functions collide, which means that they're equal to each other!

But here's the 2nd example below!

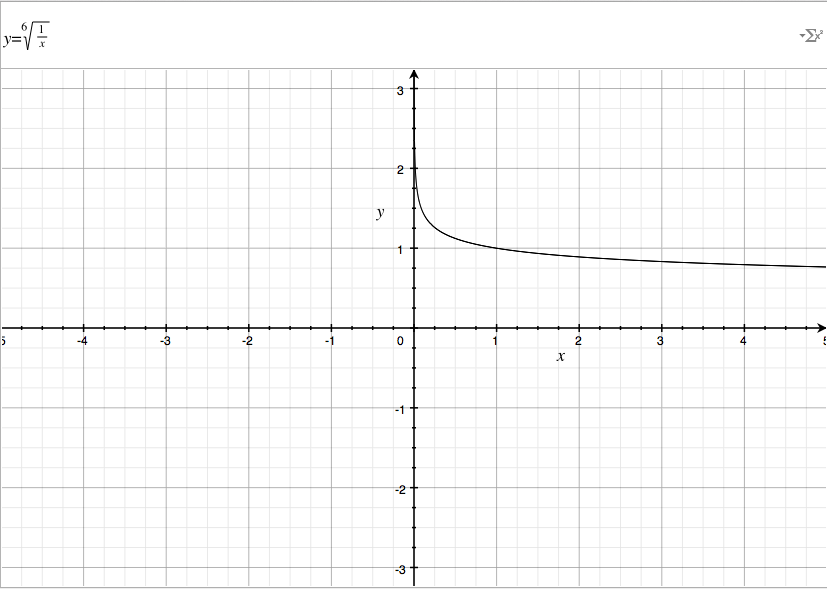
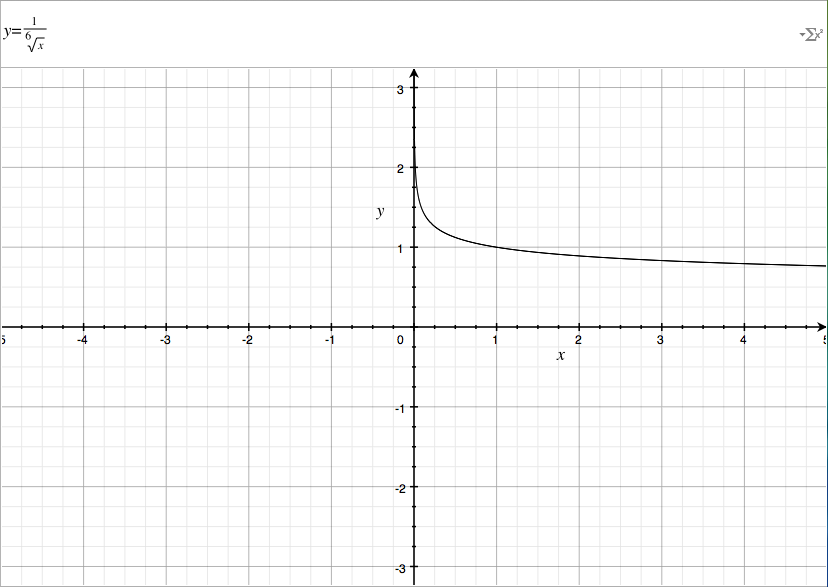
I doubled z = 3 from the 1st example to make it equal to 6 in this example. If z is even, then the function will only print on the positive sides of the domain(based on x) & range(based on y). If z is odd, it'll also print on the negative sides.

One more thing to explain before I conclude this Web page, the bigger the variable z is, the more the function's curves stretch out! Observe below:

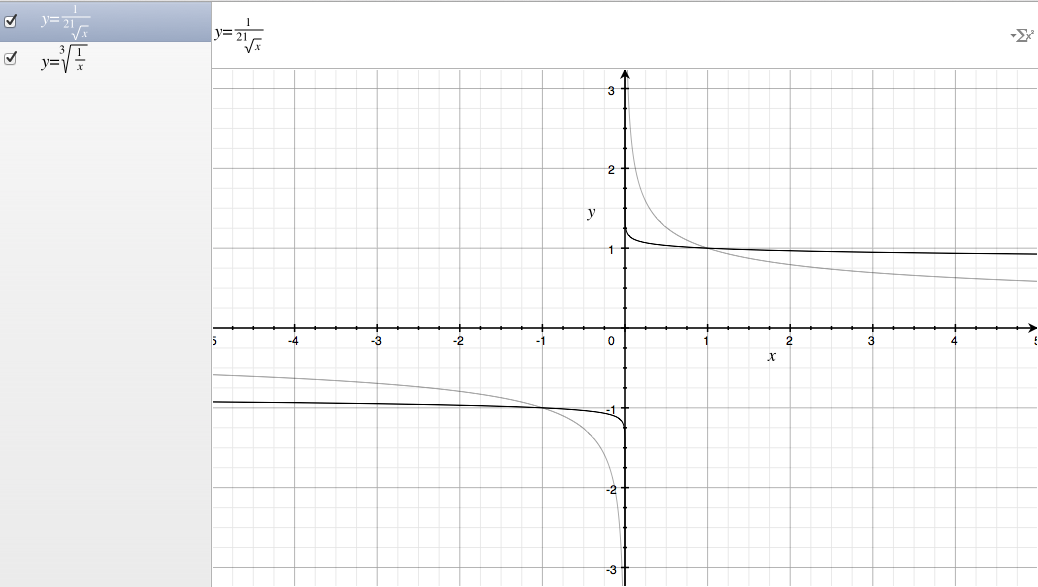
The curves in gray represent the function when z = 3 versus when z = 21.

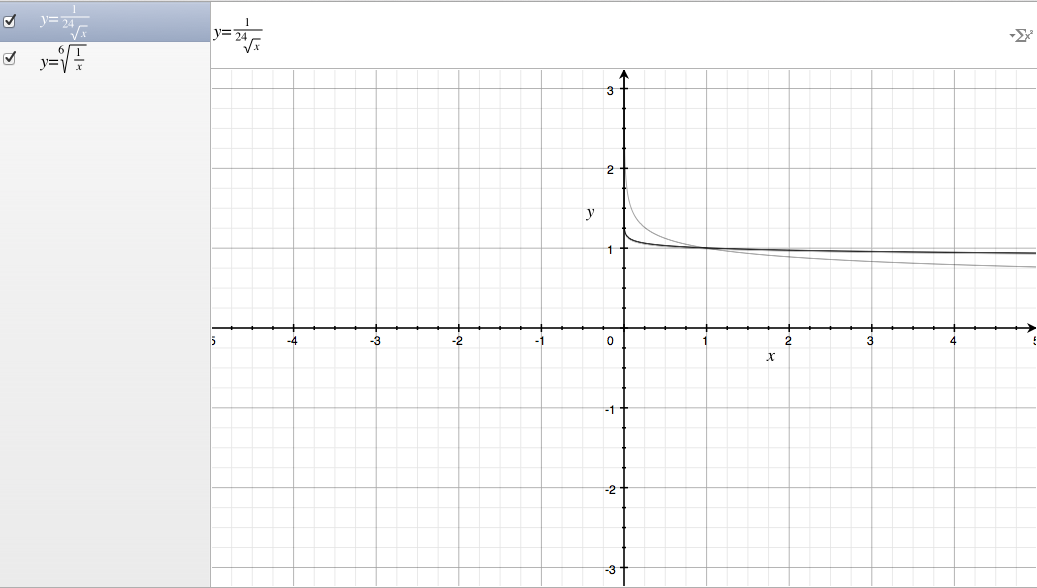
The curves in gray represent the function when z = 6 versus when z = 24. If I picked differences between even vs. odd, you would also see an extra gray curve on one side!

Back to Index Page Back to Math Trick Menu