Super Summation 2

A summation will always give you zero if the number above the summation sign (sigma) & the one below are additive inverses!

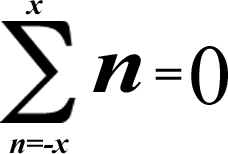
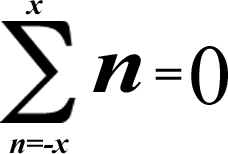
(Of course the negative number always has to be below the sigma!)

Examples:

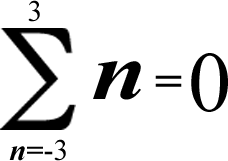
(-3) + (-2) + (-1) + 0 + 1 + 2 + 3 = 0

[All of the additive inverses cancel each other out & leave you with zero!]

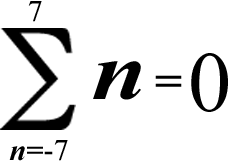
The negative numbers are put in parentheses to prevent confusion with addition or subtraction.

(-7) + (-6) + (-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 = 0

[All of the additive inverses cancel each other out & leave you with zero!]

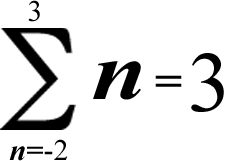
If you don't pick the right additive inverse, you won't get zero; however, something else happens...

(-2) + (-1) + 0 + 1 + 2 + 3 = 0 + 3 = 3

[The additive inverse of 3 was excluded this time, so you had to add 3 to zero, which of course gives you 3]

Zero is the number of additive identity; adding it to any number gives you no change!

If you can see her, this character's name is Miss Zero Digit.

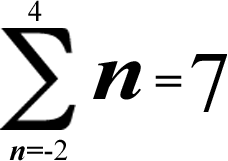
(-2) + (-1) + 0 + 1 + 2 + 3 + 4 = 3 + 4 = 7

[The additive inverses of 3 & 4 were excluded; the positive numbers added up to 7]

If you exclude more than 1 additive inverse, the remaining positive or negative numbers will add up to their respective sums!

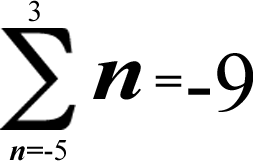
(-5) + (-4) + (-3) + (-2) + (-1) + 0 + 1 + 2 + 3 = (-5) + (-4) = -9

[The additive inverses of -5 & -4 were excluded; the negative numbers added up to -9]

If you have more positive integers left, the sum will be positive; if you have more negative integers left, the sum will be negative. In other words, the greater absolute value will reign supreme!

By the way, the number zero is its own additive inverse, just as how the number one is its own multiplicative inverse!

Back to Index Page Back to Math Trick Menu